Image credit: Jonathan Walker.
我们在归一化光谱下面讨论。
谱线的转移方程
主要参考第七章的东西。大气连续谱上有吸收和发射,那么谱线也有。
令\(l_\nu\)为谱线吸收系数,\(j^l_\nu\)为谱线发射系数;对于连续谱这两个量是\(\kappa_\nu, j^c_\nu\)。那么对于式子\((7.1)\),我们还有同样的形式:
\[\begin{align} \frac{dI_\nu}{d\tau_\nu} &= -I_\nu + \frac{j^l_\nu + j^c_\nu}{l_\nu + \kappa_\nu} \\ &= -I_\nu + S_\nu \end{align} \tag{13.3}\]只是这时候光深\(S_\nu\)包含了谱线和连续谱的部分,变成了\(\frac{j^l_\nu + j^c_\nu}{l_\nu + \kappa_\nu}\)。同样光深也要包含谱线的贡献:\(d\tau_\nu = (l_\nu + \kappa_\nu) \rho dx\)。
因为光深还是\(S_\nu\),所以大气辐射转移的基本式子\((7.4), (7.9)\)以及它们有关恒星表面的推论\((7.10), (7.15)\)仍然成立,就不抄过来了。
如此这般,这般如此,我们的主要任务还是回到了如何求新的源函数上。
谱线的源函数
我们先定性的看谱线形成的深度。利用灰大气假设,我们有
\[S(\tau_\nu) = \frac{3F_\nu(0)}{4\pi}(\tau_\nu+\frac{2}{3}) \tag{13.7}\]形式和\((7.34)\)是完全一样的,只不过虽然连续谱和波长无关,谱线却和波长有关,所以\(\nu\)的下标回来了。这个式子告诉我们光深越大的时候源函数越大(大气底层发射更多嘛),同时\(F_\nu(0)\)也与光深成正比。这就说明了谱线中心所对应的光深比较小,形成场所在大气较上层;而谱线的边缘所对应的光深比较大,形成场所在大气较下层。
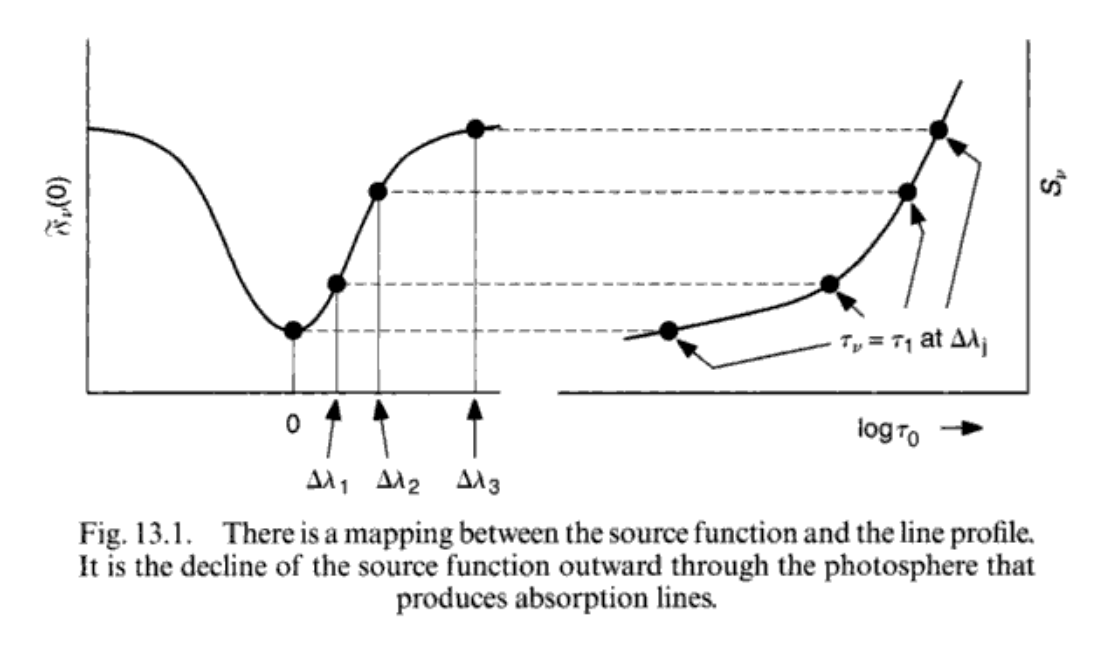
当然这个只是定性的分析,实际定量的要这么做:
我们引入谱线的发射和吸收轮廓\(\psi(\nu), \phi(\nu)\),并且加在\((5.16), (5.17)\)上面:
\[j^l_\nu \rho = N_u A_{ul} \psi(\nu) h\nu\] \[l^l_\nu \rho = N_l B_{lu} \phi(\nu) h\nu - N_u B_{ul} \phi(\nu) h\nu\]所以源函数就是
\[S_l = \frac{j^l_\nu}{l^l_\nu} = \frac{N_u A_{ul} \psi(\nu) h\nu}{N_l B_{lu} \phi(\nu) h\nu - N_u B_{ul} \phi(\nu) h\nu}\]把\((6.8)\)拿过来消掉所有的AABB:
\[S_l = \frac{2h\nu^3}{c^2} \frac{1}{(N_l/N_u)(g_u/g_l)-1}\frac{\psi(\nu)}{\phi(\nu)} \tag{13.9}\]这就是non-LTE下的源函数。
如果在LTE下并且有细致平衡原理的话,吸收发射轮廓相等并且有\((1.17)\),则
\[S_l = \frac{2h\nu^3}{c^2} \frac{1}{e^{h\nu/kT}-1} = B_\nu(T) \tag{13.10}\]就比较简单了。
[2018.9] LTE的东西当然比较好用,不过最近在华沙的一个Gaia Workshop里面Maria Bergermann把LTE批判了一番,说nLTE对于元素丰度确定来说很重要。
[2019.6] 天可怜见我现在也开始搞nLTE啦….
nLTE下的源函数
假设我们已知发射/吸收轮廓(或者它们比较好确定?),\((3.19)\)剩下的东西就是\((N_l/N_u)\)了。在稳态下处于某个能级的原子数量是不变的,所以有
\[\frac{dN_j}{dt} = \sum^M_{i=1}(N_iP_{ij} - N_jP_{ji}) = 0 \tag{13.11}\]也是守恒嘛。那这俩概率\(P\)怎么求呢?它们包含了辐射跃迁的概率以及碰撞跃迁的概率:
\[P_{ij} = 4\pi A_{ij} + 4\pi B_{ij} \int_0^\infty J_\nu\phi(\nu)d\nu + C_{ij} \tag{13.12}\]就是概率=自发的+受激的+碰撞的呗。当然\(i \ne j\),\(i \lt j\)时\(A_{ij}\)就没了。
类似的对于\(P_{ji}\)也有相似的形式,只不过\(i \lt j\)变成了\(i \gt j\)。有了这一堆\(P\)之后我们就可以解方程\((3.11)\)了。
所以我们可以从这里看出来想求\(S_\nu\)我们需要\((N_l/N_u)\),从而需要一堆\(P\),从而需要\(J_\nu\),从而需要\(S_\nu\)。循环了怎么办?迭代呗。
还有一些东西
实际上什么时候是LTE,什么时候是nLTE呢?大致来说,恒星大气内部是LTE,外部是nLTE。这其实很好理解,因为内部密度大,基本上能把里面来的光全部吸收掉再发射,就LTE了;而大气外部密度下降,就会有光子逃逸,所以就会逐渐偏离LTE。同时光子逃逸说明外层原子发射的光子变少了,源函数减小,并且原子逐渐变为吸收源,为谱线中心的吸收作出了贡献。
这个结论同时也可以有一个有趣的推论:谱线中心是nLTE的,而线翼是LTE的。一个例子是太阳的Na D线。
LTE下的谱线轮廓计算
No more nLTE things. 究竟什么时候LTE是好的得通过实际比较才能知道,或者问Maria去。
实际计算用的是\((9.13)\):
\[F_\nu = 2\pi \int_{-\infty}^{\infty} B_\nu(\tau_0) E_2(\tau_\nu) \frac{\kappa_\nu(\tau_0)\tau_0 d\log{\tau_0}}{\kappa_0(\tau_0)\log{e}} \tag{13.15}\]如果你想算\(\tau_\nu\)的话,把上式\(E_2(\tau_\nu)\)那堆积分就行了,就是\((13.16)\)。
有一个有用的推论就是:当谱线比较弱的时候,谱线的轮廓和吸收系数的轮廓是一样的。
令\((13.7)\)中的\(\tau_\nu = (4\pi-2)/3 = \tau_1\),有
\[S_\nu(\tau_1) = F_\nu(0) \tag{13.8}\]那么
\[\frac{F_c - F_\nu}{F_c} \approx \frac{S_\nu(\tau_c=\tau_1) - S_\nu(\tau_\nu=\tau_1)}{S_\nu(\tau_c=\tau_1)} \tag{13.17}\]\(\tau_c,\tau_\nu\)指的是没有/有谱线下的光深,并且LTE下谱线以及连续谱的源函数都是黑体辐射函数。
现在的光深变为:
\[\tau_\nu = \int_0^{\tau_0} \frac{l_\nu}{\kappa_0}dt_0 + \int_0^{\tau_0} \frac{\kappa_\nu}{\kappa_0}dt_0 = \tau_l + \tau_c\](不熟悉的话参见第九章\((9.13)\)后面的式子)
简化,假设\(\frac{l_\nu}{\kappa_0}, \frac{\kappa_\nu}{\kappa_0}\)与光深无关,有\(\tau_l = \frac{l_\nu}{\kappa_0}\tau_0, \tau_c = \frac{\kappa_\nu}{\kappa_0}\tau_0\)。
\(S_\nu(\tau_\nu=\tau_1) = S_\nu(\tau_l+\tau_c=\tau_1) = S_\nu(\tau_c=\tau_1-\tau_l)\)以及\(\tau_l \ll \tau_c\),泰勒展开有:
\[S_\nu(\tau_\nu=\tau_1) = S_\nu(\tau_c=\tau_1) + \frac{dS_\nu}{d\tau_c}(-\tau_l) + ...\]所以\((13.17)\)变为
\[\frac{F_c - F_\nu}{F_c} \approx \frac{\tau_l}{S_\nu(\tau_c=\tau_1)} \frac{dS_\nu}{d\tau_c}|_{\tau1} = \tau_l \frac{d\ln{S_\nu}}{d\tau_c}|_{\tau1}\]将\(\tau_l = \frac{l_\nu}{\kappa_0}\tau_0\)代入,有
\[\begin{align} \frac{F_c - F_\nu}{F_c} &\approx \frac{l_\nu}{\kappa_0}\tau_0 \frac{d\ln{S_\nu}}{d\tau_c}|_{\tau1} \\ &= \frac{l_\nu}{\kappa_\nu}\tau_c \frac{d\ln{S_\nu}}{d\tau_c}|_{\tau1}\\ &= \text{constant} \frac{l_\nu}{\kappa_\nu} \tag{13.19} \end{align}\]就是这样。
谱线的贡献函数
“王老五就是未结婚的王老五”,贡献函数就是第九章的贡献函数。不多说了,放两张图自己体会。
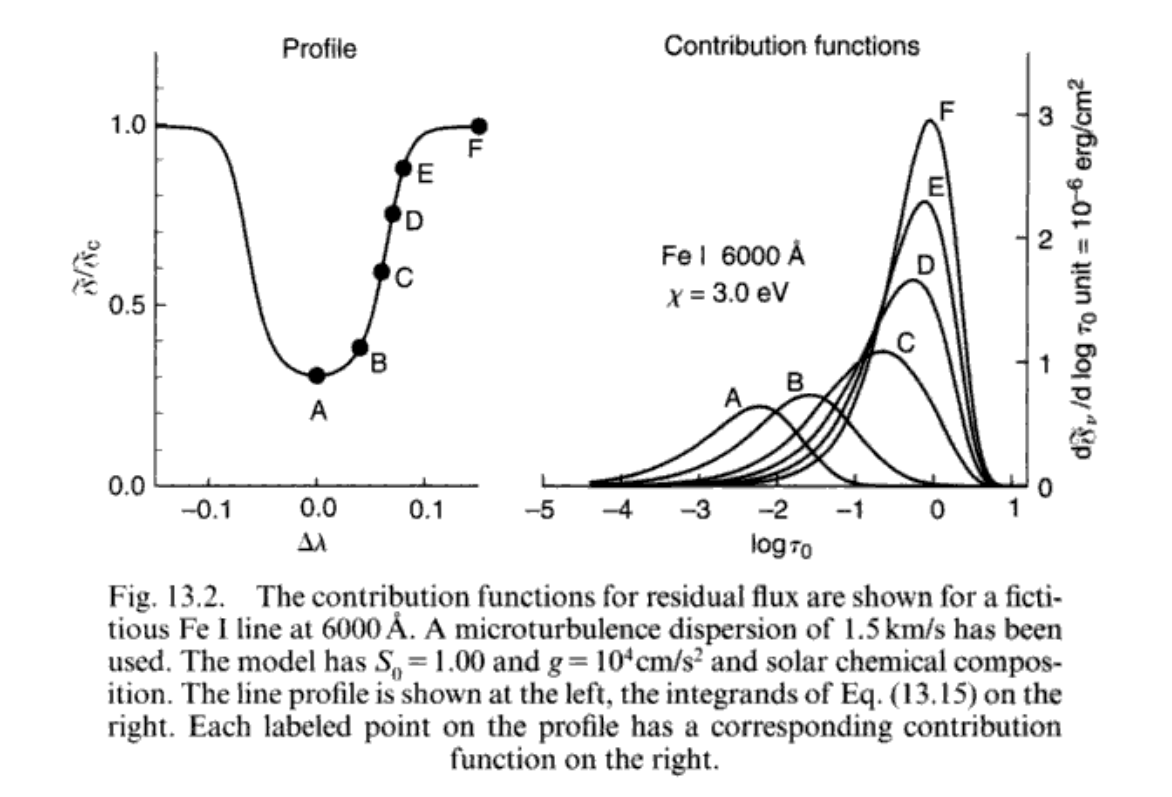
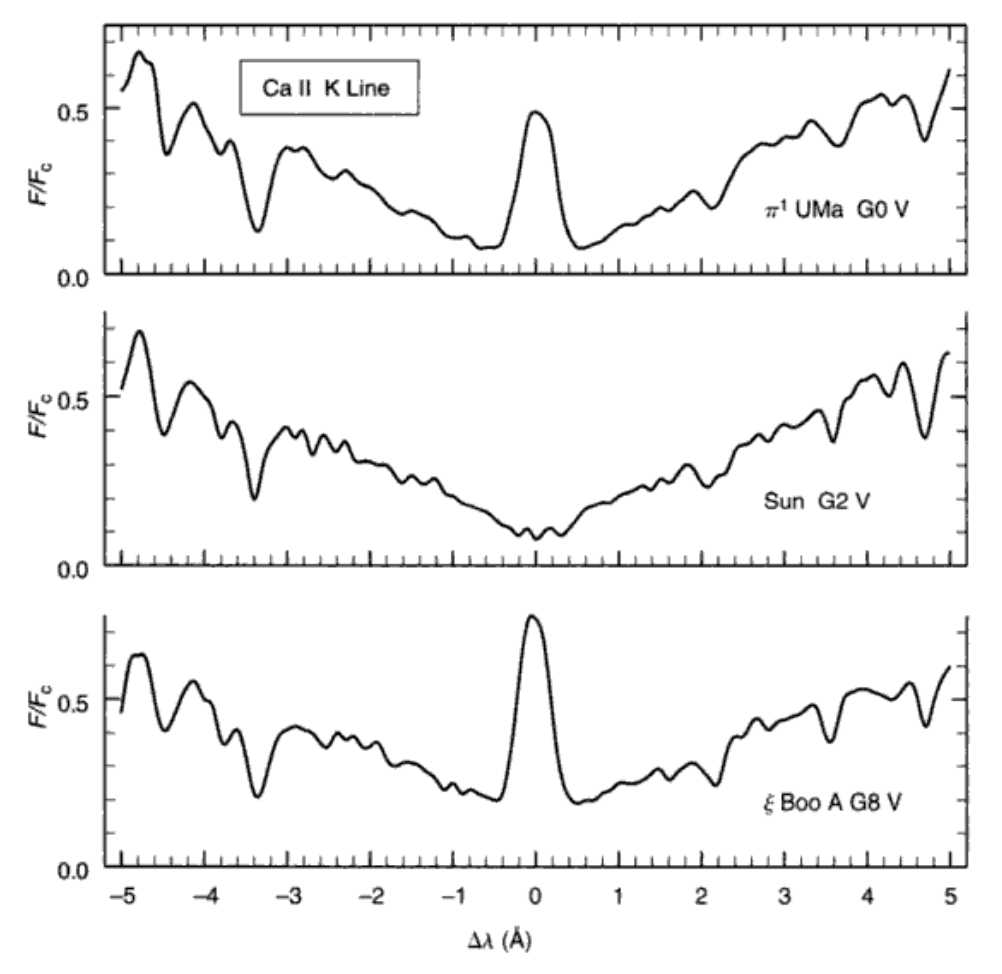
谱线强度的行为
这里只讨论几个对谱线强度有比较大影响的参数:温度、\(\log{g}\)以及金属丰度。
温度
对于弱线来说,温度变化影响了原子的占据数以及跃迁、连续谱的吸收,从而改变了谱线强度。强线以及氢线的话,还要考虑\(\gamma\)随温度的变化。
这里姑且只讨论弱线,则有下图:
首先由\((8.12)\)有:
\[\kappa_\nu = \text{constant} T^{-5/2} P_\mathrm{e} e^{0.75/kT}\]Case 1时,是原子谱线+中性原子:
\[N_l = \text{constant} N_0 e^{-\chi/kT} \approx e^{-\chi/kT}\] \[\Rightarrow R = \frac{l_\nu}{\kappa_\nu} = \text{constant} \frac{T^{5/2}}{P_\mathrm{e}} e^{-(\chi+0.75)/kT} \tag{13.20}\]又因为\((9.27)\),有:
\[\ln{R} = \text{constant} +2.5 \ln{T} - \frac{chi+0.75}{kT} -\Omega T\]其他Case类似,具体公式请看书。要留意Case 1和4的表达式是完全一样的,但是因为温度范围不同趋势不同。
压力
有三种:1. 电离平衡改变导致谱线/连续谱吸收原子数改变; 2. damping常数与与压力有关; 3. 线性斯塔克效应。
这里的讨论都基于\((13.19)\);低温时\(\kappa_\nu \propto P_\mathrm{e}\),高温时\(\kappa_\nu \propto \text{constant}\)。
第一种:
\[l_\nu \propto N_i\] \[\frac{N_{r+1}}{N_r} = \frac{\Phi(T)}{P_\mathrm{e}}\]实际上是原子电离的Saha方程\((1.20)\)。
当跃迁是发生在\(r\)电离态而多数原子在\(r+1\)电离态的时候,\(l_\nu \propto P_\mathrm{e}\);当跃迁是发生在\(r+1\)电离态而多数原子在\(r+1\)电离态的时候,\(l_\nu \propto \text{constant}\)。当跃迁是发生在\(r+1\)电离态而多数原子在\(r\)电离态的时候,\(l_\nu \propto P_\mathrm{e}^{-1}\)。
第二种主要作用于线翼处,\(l_\nu \propto \gamma = \gamma_6 + \gamma_4 + \gamma_\mathrm{nat}\)
第三种主要影响氢线,\(l_\nu \propto P_\mathrm{e}\)。
再往高温走,电子散射会比较重要,所以由\((8.17)\)有
\[\kappa_\nu \approx \kappa_\mathrm{e} = \frac{\alpha(e)P_\mathrm{e}\sum A_j}{P_\mathrm{g}-P_\mathrm{e}}\]此时\(P_\mathrm{g} \approx 2P_\mathrm{e}\),所以\(\kappa_\nu\)独立于\(P_\mathrm{e}\);同时\(l_\nu \propto P_\mathrm{e}^2\)(哪来的?)
金属丰度
生长曲线。
简单地来说,我们考虑这么一个图像:连续谱光源在后面,前面是一团冷的气体,厚度为\(L\)。
\[F_\nu = F_c e^{-\tau_\nu} \tag{13.28}\] \[\tau_\nu = \int_0^L l_\nu \rho dx = \int_0^L N \alpha dx = A \int_0^L (N/N_E) N_\mathrm{H} \alpha dx \tag{13.29}\]\(N\)为吸收原子个数,\(N_E\)为这种原子的总个数。
当\(\tau_\nu \ll 1\),即谱线很弱的时候,我们有
\[F_\nu \approx F_c(1-\tau_\nu)\]所以这个时候线深和谱线强都都正比于\(A\)。
对于强线来说,我们需要考虑线翼;结论是
\[W = (\langle\gamma\rangle Afh)^{1/2} \int_0^\infty (1-e^{-1/u^2})du \tag{13.31}\]这里的生长曲线指的是仅仅改变某个元素的丰度;而如果我们改变整个恒星的金属丰度的话,生长曲线会不一样;这是因为改变整体的丰度会改变电离平衡、连续谱吸收以及碰撞的damping。一个例子如下图:
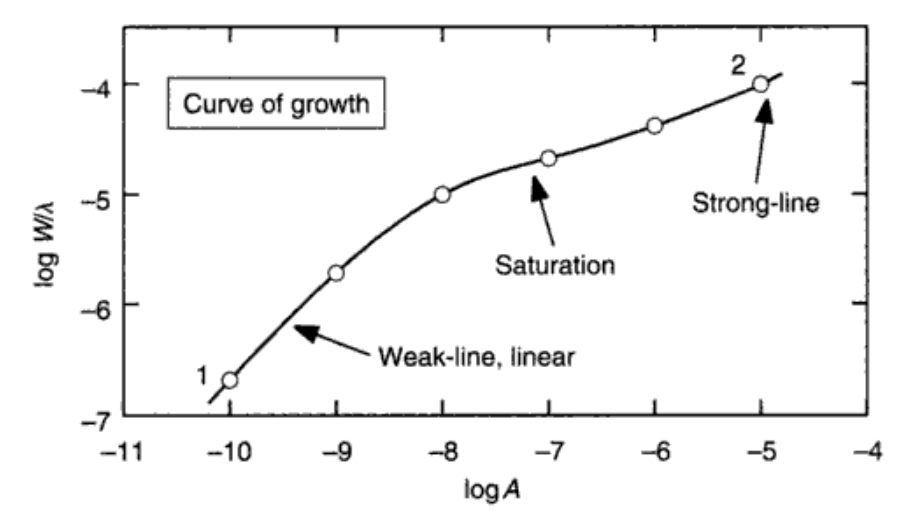
对于实际的谱线来说,例子如下:
图三张
最后的碎碎念
LTE和nLTE都有可能出错
图两张
它们都需要致宽;就连生长曲线都会受到致宽的影响(为什么?)