题图Credit：Kravchenko+2018.
谱线是在哪里形成的？搜了一些看了一些论文之后这个问题变成了谱线究竟是在哪里形成的？
其实这不是一个很复杂的问题，不过不同人有不同的解决方式，所以哪种是最好的，以及在什么情况下适用是需要总结一下的。看完这篇之后很多论文就不用看了。
我们要解决什么问题？
这不是废话嘛，谱线在哪里形成的。那么这个问题应该如何放入在我们的恒星大气模型中呢？又回到干啥都能拿出来讲的这张图了：
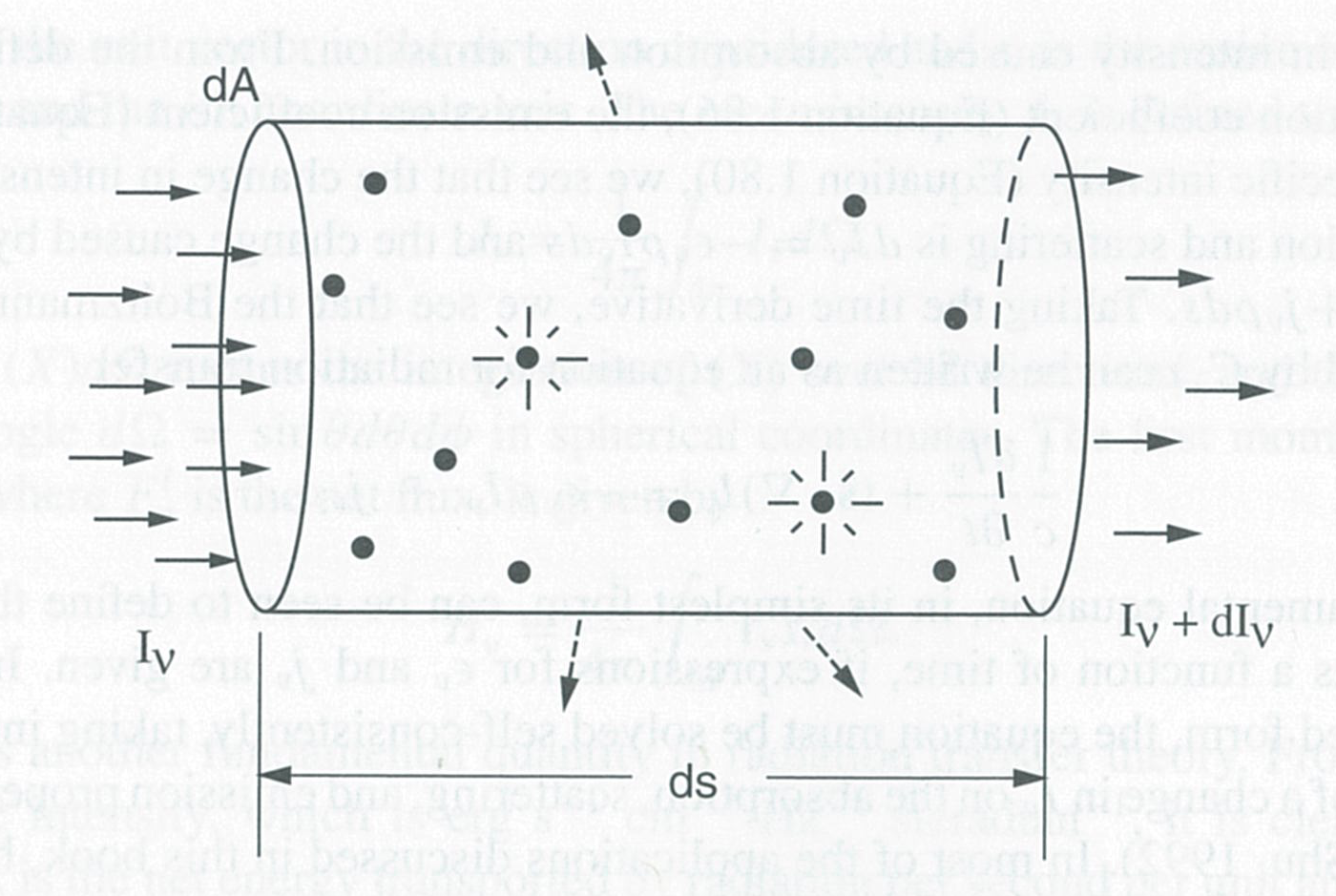
啊你看左边来的星光在中间被吸收和散射然后往右边射出，在这个过程中光的总量发生了变化，不就产生了吸收了么。所以将左边入射的星光看作外部光源、中间的管子看作恒星大气、右边出射的光看作我们观测到的光，那么谱线就是在这根管子里形成的。当然啦并不是管子的每一处都会形成谱线的，靠近内部的一侧（左侧）温度很高，这里辐射和吸收达到平衡，所以没有谱线形成（吃多少吐多少当然没有光强变化）；外部一侧（右侧）密度太低，吸收光的原子就很少了，自然也不属于谱线形成的区域。
澄清以及延伸：
- 星光怎么是外部光源：这里的模型是恒星的连续谱是从一个内部的球面发出来的，然后打到球面外面的大气层里面；这个模型肯定不怎么准确（并且不同的波长上连续谱的位置也不一样），但是理解来说够用了。
- 管子一定处于恒星大气中吗：不一定。最极端的例子是telluric线，它的连续谱是恒星，但是吸收（也就是形成）的区域是在地球大气上，一个天一个地。
所以要解决这个问题，我们要找到一个东西，它以恒星大气的位置坐标（高度或者光深）为自变量，它的值代表着在这个地方上对某个量的贡献是多少。这其实就是找到一个对光深的积分，积分之后的值就是我们的目标参数。这就好办了。
光强的贡献函数
正巧，我们在解辐射转移方程的时候有过这个东西。参考OASP7，我们有辐射转移方程:
\[\frac{dI_\nu}{d\tau_\nu} = -I_\nu + S_\nu\]以及\((7.8)\)
\[I_\nu(0) = \int_0^{\infty} S_\nu e^{-\frac{\tau_\nu}{\mu}} \frac{d\tau_\nu}{\mu}\]这就可以了，\((7.8)\)是符合我们上一节对贡献函数的要求的，所以它在积分号和\(d\tau_\nu\)之间的东西就是贡献函数：
\[C_I = \frac{1}{\mu} S_\nu e^{-\frac{\tau_\nu}{\mu}}\]它代表的是在\(\tau_\nu\)处的辐射对光强的贡献；其实也很好理解，因为源函数就是发射相对于吸收的归一化量，在\(\tau_\nu\)处的发射往外跑的时候被吸收，到最后打了个\(\frac{1}{\mu} e^{-\frac{\tau_\nu}{\mu}}\)的折扣，就完了。
再稍微强调一下，贡献函数的形式就和\(C_I\)差不多，需要符合目标参数\(q_\nu(0) = \int_0^{\infty} C_q \frac{d\tau_\nu}{\mu}\)的形式；而一旦有了目标参数的辐射转移方程\(\frac{dq_\nu}{d\tau_\nu} = -q_\nu + S_\nu\)，我们就可以仿照光强的贡献函数写出相应的\(C_q\)来了。当然仿照的过程中需要相应地改\(\tau_\nu, S_\nu\)。
例子：PANDORA或者MOOG
光强减少的贡献函数
上面光强的源函数只为我们计算谱线形成范围提供了一个范本，并没有给出最终的解决方案；因为光强的产生并不代表着谱线的形成。我们平常看到的谱线是吸收线，也就是说光强减少的贡献函数才和谱线形成区域相关联。那怎么办呢？Magain 1986给出了答案：对着上一节照板煮糊。
我们现在关心的参量是光强的减少：
\[R_I = \frac{I_c-I_t}{I_c}\]原文的\(I_t\)用的是\(I_l\)，不过为了统一我都用\(I_t\)。顾名思义\(I_c\)是谱线不存在时的光强，\(I_t\)是谱线存在时的光强。用\(I_t\)表示的好处在于这个量不单纯表示谱线吸收之后的光强，它是连续谱和谱线共同作用下的光强。不过看不懂不要紧，后面会把这个问题说清楚的。
将\(R_I\)对\(z\)求导，有：
\[\frac{dR_I}{dz} = \frac{I_t}{I_c^2} \frac{dI_t}{dz} - \frac{1}{I_c} \frac{dI_t}{dz}\]而对着\(I_c, I_t\)可以分别写出各自的辐射转移方程：
\[\begin{align} \mu \frac{dI_t}{dz} &= -\kappa_c \rho (I_c - S_c) \\ \mu \frac{dI_c}{dz} &= -(\kappa_c + \kappa_l) \rho (I_t - S_t) \\ S_t &= \frac{\kappa_c S_c + \kappa_l S_l}{\kappa_c + \kappa_l} \\ \end{align}\]这里出现了下标为\(l\)的量，不过是没有错的。把后面两条式子代进第一条里面去，可得：
\[\begin{align} \frac{\mu}{\rho} \frac{dR_I}{dz} &= -\kappa_{R_I} (R_I - S_{R_I}) \\ \kappa_{R_I} &= \kappa_l + \kappa_c \frac{S_c}{I_c} \\ S_{R_I} &= \frac{1-\frac{S_l}{I_c}}{1+\frac{\kappa_c S_c}{\kappa_l I_c}} \\ \end{align}\]然后就可以写出\(R_I\)的表达式以及贡献函数了：
\[R_I(0) = \int_0^\infty \frac{1}{\mu} S_{R_I} e^{-\frac{\tau_{R_I}}{\mu}} d\tau_{R_I}\] \[C_{R_I} = \frac{1}{\mu} S_{R_I} e^{-\frac{\tau_{R_I}}{\mu}}\]流量减少的贡献函数？
我们还没完。光强的减少虽然是可观测量，但是那是太阳的可观测量；对于恒星来说，我们只能观测到流量。那流量减少的贡献函数可不可以通过类似的方法给出呢？不好说；Achmad 1991给出了一些讨论以及另一个解决方案。
如果我们类似定义\(R_F = 1- F_t / F_c\)的话，我们的确可以给出相应的\(\kappa_{R_I}, S_{R_I}\)。但是它们不是唯一的，只要符合条件的\(\kappa_{R_I}, S_{R_I}\)们都可以用；更要命的是不同\(\kappa_{R_I}, S_{R_I}\)的贡献函数很不一样，有的在-1那有峰，有的在-2那。Magain 1986规定的是\(S_R\)中不可以显含和总量有关（也就是带下标\(t\)）的量；这个也能理解，不过在\(R_F\)中就不好做了。
那怎么办？数学走不通的这个时候就要回到我们的物理图景去找新的路子了。谱线是在第一节图中的管子里形成的，谱线形成的具体过程包括吸收和发射；我们想把谱线吸收+发射对连续谱的影响作为目标参量但是失败了，那么可不可以退而求其次，把谱线的吸收或者发射作为目标参量呢？吸收可能不好做，那谱线发射总可以吧？思路就是这样的了。恒星发出的流量如下：
\[\pi F_t(0) = \int I_t \cos{\theta} d\omega\]这当然没啥用处，又不是对光深积分；但是我们正好也有个光深积分积出来是流量的玩意儿：
\[\begin{align} F_t(0) &= \int_0^\infty S_t(\tau_\nu) E_2(\tau_\nu) d\tau_\nu \\ E_2(\tau_\nu) &= \int_1^\infty \frac{e^{x\tau_\nu}}{x^2} dx \\ \end{align}\]就是OASP7中\((7.15)\)的E积分。这就好了，我们可以马上高兴地写出\(F_t\)的贡献函数：
\[C_{F_t} = S_t(\tau_\nu) E_2(\tau_\nu)\]不过是不是高兴得太早了一点？说好的谱线发射的流量呢？此时只需简单地将源函数\(S_t\)拆成谱线的和连续谱的两部分：
\[S_t = \frac{\sum j_i}{\kappa_t} = \frac{\kappa_l}{\kappa_t}S_l + \frac{\kappa_c}{\kappa_t}S_c\]就可以写出连续谱和谱线发射的贡献函数：
\[\begin{align} C_{F_l} = \frac{\kappa_l}{\kappa_t} S_l(\tau_\nu) E_2(\tau_\nu) \\ C_{F_c} = \frac{\kappa_c}{\kappa_t} S_c(\tau_\nu) E_2(\tau_\nu) \\ \end{align}\]谱线的发射和谱线的吸收仍然不是同一个东西，但是只要我们认为它们发生在同一个地方就可以了。还是下一节会详细讨论这个问题。
有了这三个贡献函数之后，我们就可以看一下它们的关系了。我们预期的是连续谱提供了光子给谱线吸收，所以谱线的吸收位置不能比连续谱的位置更靠里。
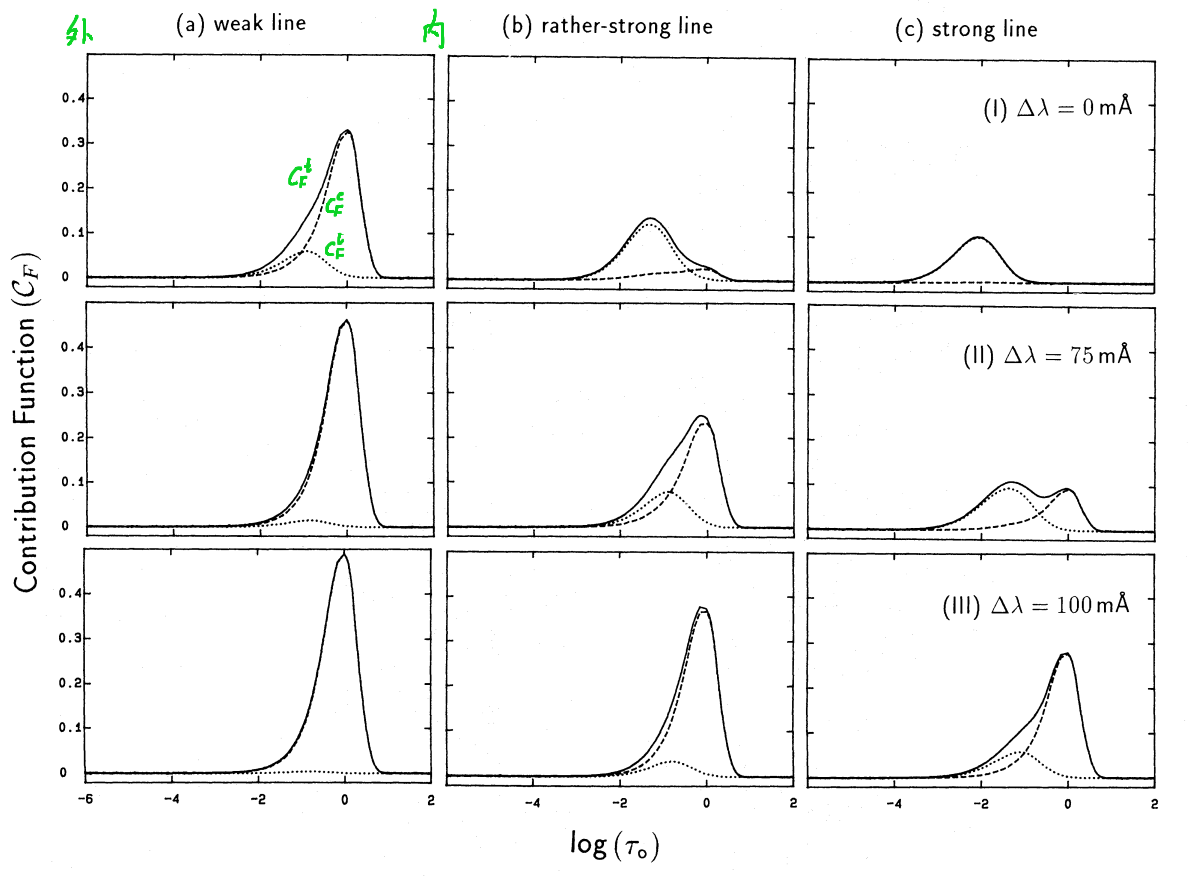Achmad 1991 图2
还是符合我们预期的；而强线因为吸收太多，基本上所有的流量都是从谱线那来的，就没有连续谱了。
那这个贡献函数和Magain 1986的贡献函数一样吗？请看下图：
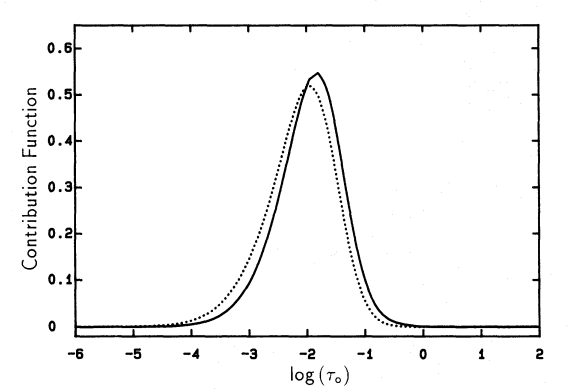Achmad 1991 图3
基本上是一样的。
究竟哪些能用哪些不能用？
我们把这个问题说清楚吧；在前面我们稍微将某些量区别对待，有些是我们想要的有些则不能包含在参量内。那么究竟哪些是我们要留下的哪些不是呢？Gurtovenko+1991讨论了这个问题。
我们将连续谱和谱线的过程拆开，如下图：
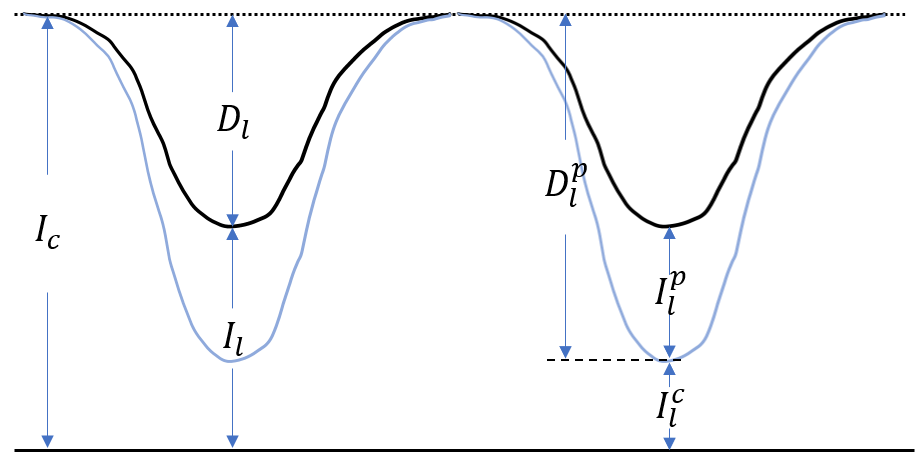Gurtovenko+1991 图1
- \(I_c\)是连续谱的发射，代表着谱线不存在时的出射光强
- \(D_l^p\)是连续谱发射通过谱线区域时被谱线吸收的量（纯吸收，谱线的发射不计算在内）
- \(I_l^c\)是连续谱发射通过谱线区域时没有被吸收的量，也就是最终谱线轮廓处连续谱光强占的比例
- \(I_l^p\)是谱线发射光强占的比例（谱线发射在这里被count了）
- \(D_l = D_l^p - I_l^p\)是最终观测到的谱线总吸收
- \(I_l = I_l^c + I_l^p\)是最终观测到的谱线总发射光强
顺便，\(D\)的意思是depression。然后我们可以写出这六个量的表达式和贡献函数了。顺便为了简化，这里只介绍solar disk center的情况，\(\mu = 1\)。
\(I_c\)
\[I_c(0) = \int_0^{\infty} S_c e^{-\tau_c} d\tau_c\]抄OASP7就完了。
\(D_l^p\)
连续谱发射通过谱线区域时被谱线吸收的量就是\(I_c\)在某一点\(\tau_c\)处乘上该处的吸收系数\(\kappa_l(\tau_c)\)再乘上这段的长度元\(\Delta h(\tau_c)\)。但是这里有一个问题，\(I_c\)是只考虑连续谱吸收发射是的光强，但是入射的时候因为\(\tau_c\)前面有谱线和连续谱的吸收，这层上面的光强和吸收量都会被它之外的大气进行消光，所以要借用\(I_c\)定义中的\(e\)指数项，再乘上一个\(e^{-(\tau_c+\tau_l)}\)，有：
\[D_l^p = \sum I_c(\tau_c) e^{-(\tau_c+\tau_l)} \kappa_l(\tau_c) \Delta h(\tau_c)\]将\(I_c\)的定义代入并定义\(\eta = \kappa_l / \kappa_c\)以及\(\kappa_l(\tau_c) \Delta h(\tau_c) = \eta(\tau_c) \Delta\tau_c\)，有：
\[D_l^p = \int_0^\infty \left[ \int_{\tau_c}^\infty S_c(\tau_c) e^{-\tau_c} d\tau_c \right] e^{-\tau_l} \eta d\tau_c\]\(I_l^p\)
谱线发射光强占的比例的定义和\(D_l^p\)差不多，有：
\[I_l^p = \sum e^{-(\tau_c+\tau_l)} \epsilon_l(\tau_c) \Delta h(\tau_c) = \sum S_l(\tau_c) e^{-(\tau_c+\tau_l)} \eta(\tau_c) \kappa_c(\tau_c) \Delta h(\tau_c)\]以防万一还是写明\(\epsilon_l = S_l \kappa_l = S_l \kappa_c \eta\)。将\(\Delta h(\tau_c)\)换成\(\Delta \tau_c\)并改成积分号，有
\[I_l^p = \int_0^\infty S_l e^{-(\tau_c+\tau_l)} \eta d\tau_c\]\(D_l\)
上面已经写了\(D_l = D_l^p - I_l^p\)，两式相减就完了：
\[D_l = \int_0^\infty \left[ \int_{\tau_c}^\infty S_c(\tau_c) e^{-\tau_c} d\tau_c - S_l(\tau_c) e^{-\tau_c} \right] e^{-\tau_l} \eta d\tau_c\]\(I_l^c\)
这玩意跟\(I_l^p\)差不多，
\[I_l^c = \sum e^{-(\tau_c+\tau_l)} \epsilon_c(\tau_c) \Delta h(\tau_c) = \sum S_c(\tau_c) e^{-(\tau_c+\tau_l)} \kappa_c(\tau_c) \Delta h(\tau_c)\]所以
\[I_l^c = \int_0^\infty S_c e^{-(\tau_c+\tau_l)} d\tau_c\]\(I_l\)
由\(I_l = I_l^c + I_l^p\)，有
\[I_l = \int_0^\infty (S_c + \eta S_l) e^{-(\tau_c+\tau_l)} d\tau_c\]它们的贡献函数就不单独列了。这些式子比较基础，即使是NLTE下也能使用；顺带一提这里的吸收/发射系数是包含了密度的，但是前面几节的没有。
搞定了这些表达式我们就可以看看这六个贡献函数线具体长什么样子了，这里仅举两例：
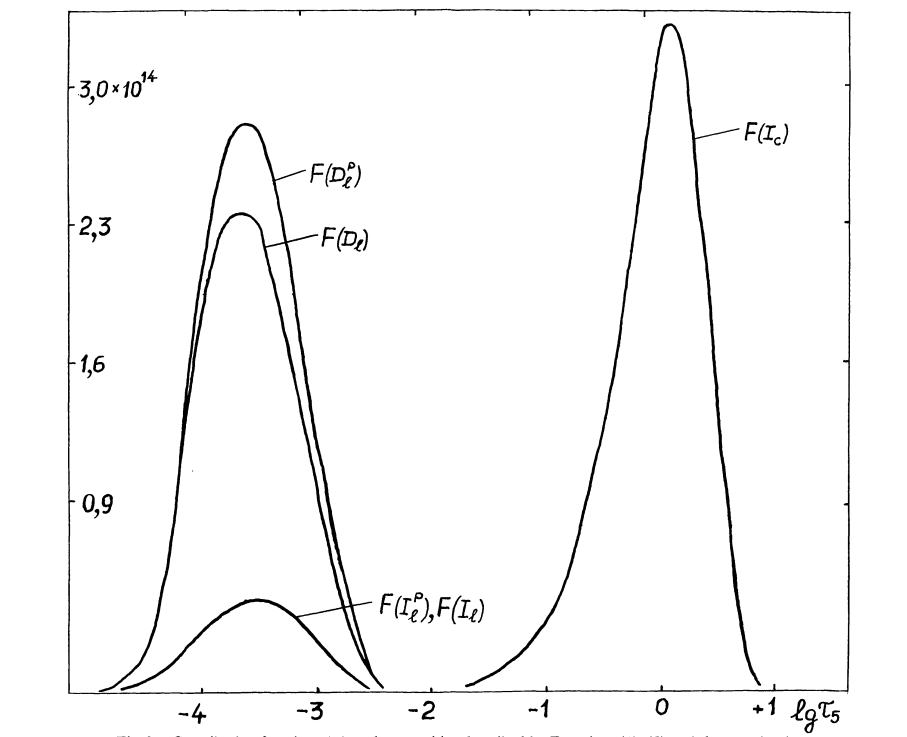Gurtovenko+1991 图2
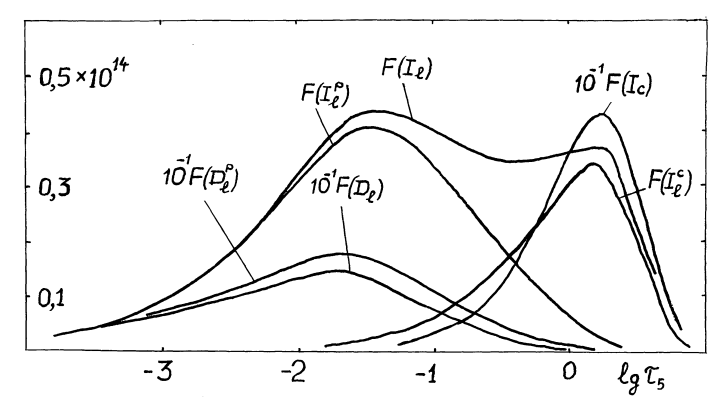Gurtovenko+1991 图4
可以看到结论是类似的，连续谱在大气底层形成，然后在上部被谱线吸收；如果吸收不多那\(CF(I_l)\)会有双峰，吸收很强的时候\(CF(I_l)\)就和谱线的贡献函数一致了。从这里也可以看出想要讨论谱线的形成区域的话，我们应该选用和谱线的贡献函数（吸收/发射都可以，\(D_l^p, I_l^p\)）或者总的吸收贡献函数\(D_l\)（因为它只算了谱线的吸收）；连续谱的贡献函数当然只对连续谱有用，而最方便能得到的\(I_l\)的贡献函数实际上受连续谱和谱线共同影响，是不能用的。
这里有一个坑，就是每个式子最后的微分变量和画图的横坐标必须要完全一致。以\(I_c(0) = \int_0^{\infty} S_c e^{-\tau_c} d\tau_c\)为例，如果横坐标为\(\tau_c\)那么这条式子即为
\[I_c(0) = \int_0^{\infty} S_c(\tau_c) e^{-\tau_c} d\tau_c\]可以直接进行计算；但是我们有的时候不知道\(S_c(\tau_c)\)或者想用别的自变量，那么就需要换算了。以几何深度\(z\)为例（PANDORA里面用的），这时的式子实际上是
\[I_c(0) = \int_0^{\infty} S_c(z) e^{-\tau_c(z)} d\tau_c(z)\]要记住\(d\)后面的微分变量必须和横坐标完全一致，所以这里需要用光深的定义\(d\tau_c(z) = \kappa_c dz\)代到式子里面去，\(S_c(z) e^{-\tau_c(z)} \kappa_c\)这个玩意儿才是贡献函数。
再举一个例子（都是自己踩过的坑…），当我们用一个参考的光深的对数\(\log{\tau_\mathrm{ref}}\)做横坐标的时候（这是MOOG用的），式子变为
\[I_c(0) = \int_0^{\infty} S_c(\tau_\mathrm{ref}) e^{-\tau_c(\tau_\mathrm{ref})} d\tau_c(\tau_\mathrm{ref})\]在这里我们要将\(d\tau_c(\tau_\mathrm{ref})\)变成\(d\log{\tau_\mathrm{ref}}\)，转换关系为\(d\tau_c(\tau_\mathrm{ref}) = \ln{(10)} \tau_\mathrm{ref} \frac{\kappa_c}{\kappa_\mathrm{ref}} d \log{\tau_\mathrm{ref}}\)。
那有人可能会疑惑前面源函数和\(e\)指数项需要把自变量换成对数的吗？其实不用直接换，因为我们之后会把横坐标取对数，这个时候就相当于把这两个项的自变量换成对数的了。
总结一下就是积分变量的源函数一般可以随便换成横坐标的量，但是剩下的特别是后面的\(d\)要换过去，对数坐标的话还要加点东西。
这里还留下了一个坑，Gurtovenko+1991光强到流量的转换没有做；如果巨星/超巨星的临边昏暗很小的话那没问题。我估计我就直接用上面的式子了。
贡献函数和恒星参数的关系
我们重于定义好了贡献函数，可以看看它们和恒星参数的关系了。
速度场
这个其实挺复杂的。直接看图吧：
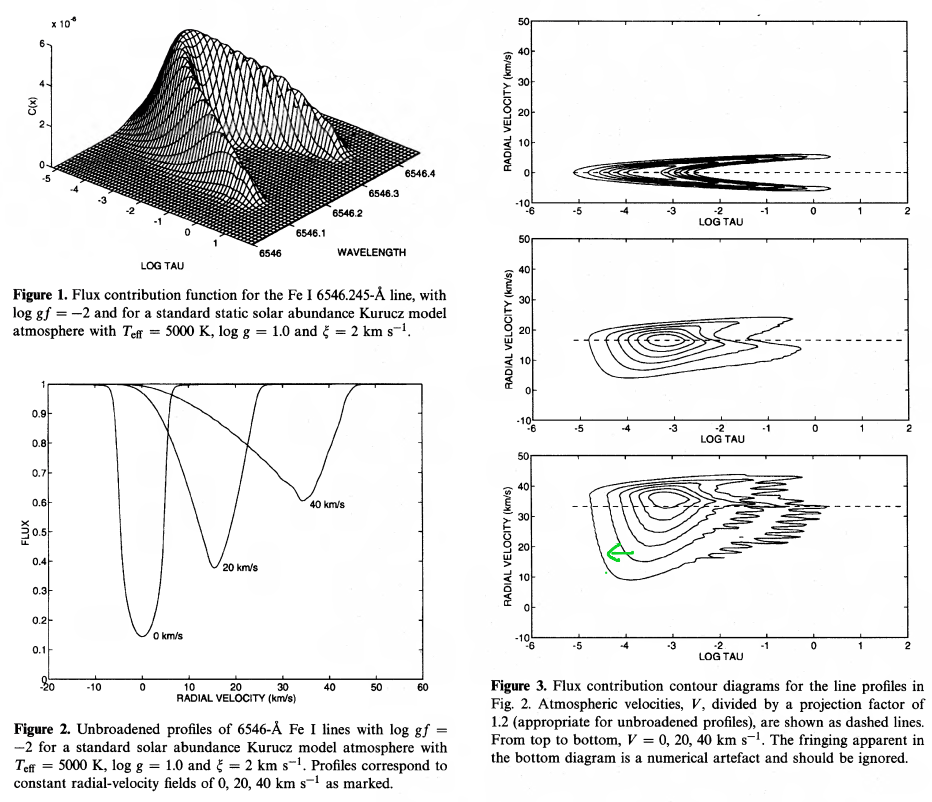Albow+1996
可以看出线翼形成于大气更深处。加上整体速度场之后因为disk center的谱线偏离了静止波长，在静止波长处我们只能看到恒星边缘（只有切向速度）的大气的谱线；而恒星边缘的连续谱形成位置更高，所以静止波长处谱线的形成位置也被相应抬高了。
激发能
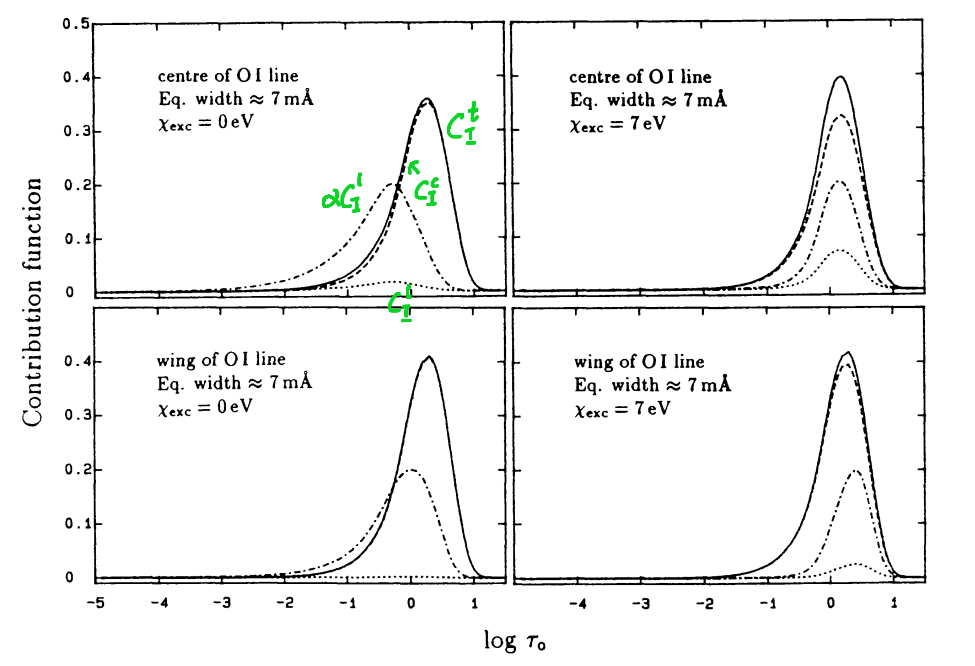Achmad 1992 图2
很好理解，激发能越高谱线越需要高温激发，就越往大气内部跑。
3D-NLTE下
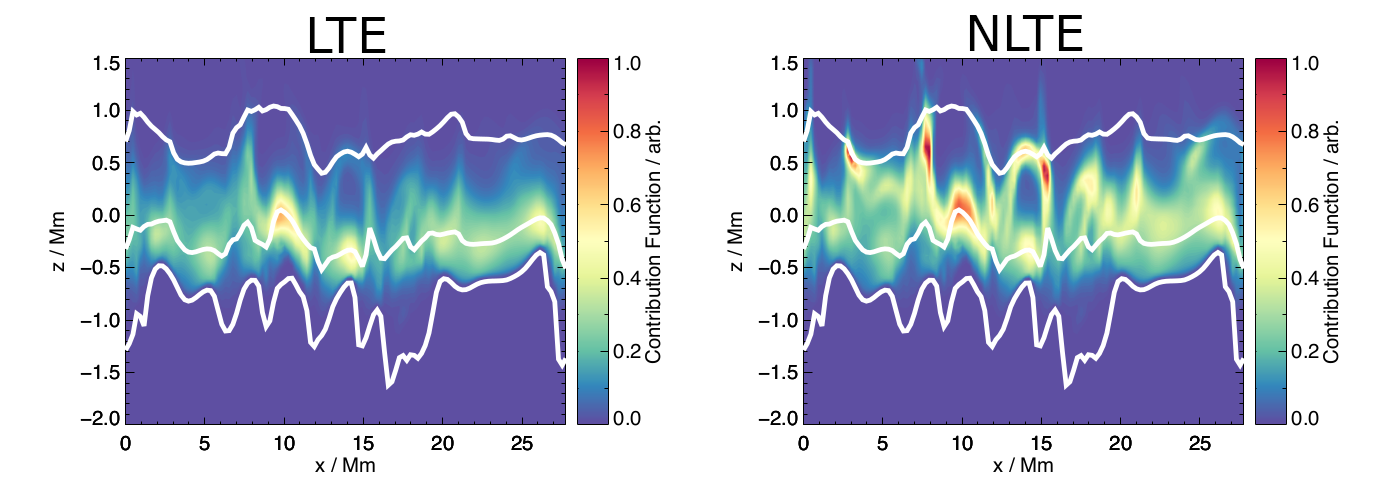Amarsi 2015 图3
这个就比较前沿了，感觉有得做。
恒星大气切片
这也是很好玩的，例子是Kravchenko+2018。反正就是挑出在不同地方形成的谱线然后测它们的波长偏离，就可以得到不同地方的RV了，对Mira什么的有用。
