这里作为星震学测量氦丰度方法的补充说明，估计会比较散。主要是看Verma+19得出的问题以及查询得到的答案。
原理
恒星内部的温度是越来越高的，而温度高到一定程度之后就会将原子电离；比如说氢原子会逐渐被剥成质子和电子，氦原子(HeI)会变成\(\mathrm{He^+}\)(HeII)和\(\mathrm{He^++}\)(HeIII)。原子电离情况和温度的关系请参照OASP1, Fig. 1.10。在这里我们主要讨论恒星内部的情况，Kippenhahn的恒星结构与演化给出了电离情况与压强的关系：
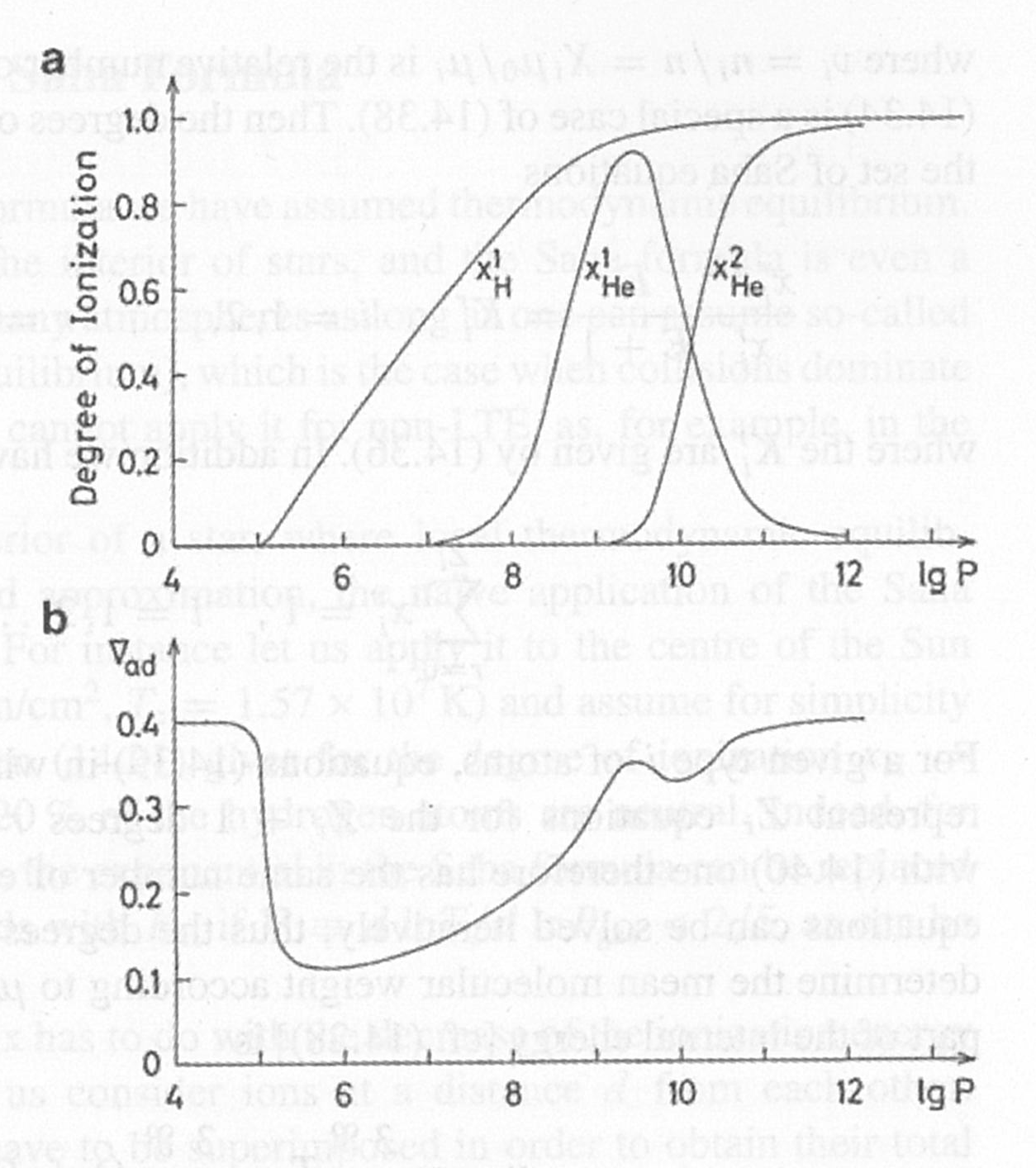Kippenhahn 恒星结构与演化 Fig. 14.1
有趣的是当HeIII开始出现的时候\(\Delta_\mathrm{ab}\)出现了一个dip；这里的\(\Delta_\mathrm{ab} = \frac{P\delta}{T\rho c_P}\)，而电离情况的变化改变了\(P\)，使得\(\Delta_\mathrm{ab}\)发生了变化。
不过这里我们的重点不在\(\Delta_\mathrm{ab}\)，而在绝热指数\(\Gamma_1 = \left( \frac{\partial \ln{P}}{\partial \ln{\rho}} \right)_s\)上，它和\(\Delta_\mathrm{ab}\)有类似的行为：
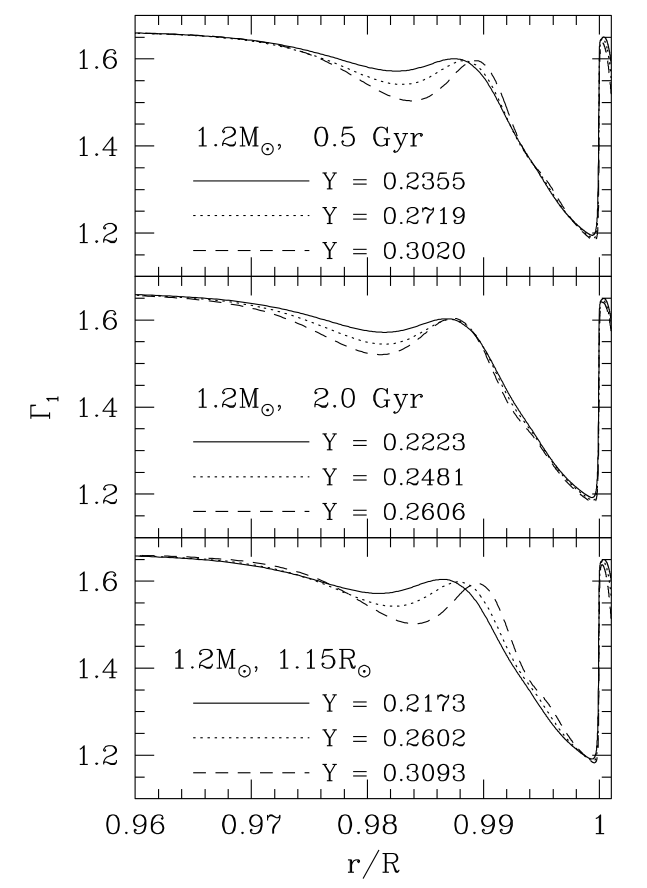Basu+04 Fig. 1
这个dip的深度和氦丰度\(Y\)是有关的，而且会对恒星的振动产生影响。具体的影响是这样的：原有的功率谱的峰的位置被稍微移动了一点，移动的频率
\[\delta \nu_\mathrm{He} = A_\mathrm{He}\nu e^{-8\pi^2\Delta_\mathrm{He}^2\nu^2} \sin{(4\pi\tau_\mathrm{He}\nu + \psi_\mathrm{He})}\]其中\(A_\mathrm{He}\)为\(\Gamma_1\)峰的面积（和氦丰度有关）、\(\Delta_\mathrm{He}\)为\(\Gamma_1\)峰的宽度、\(\tau_\mathrm{He} = \int_{r_m}^R \frac{1}{c} dr\)，为声学深度（\(c\)为声速）。
所以只要画出了频率的偏移和频率的关系，再对它进行拟合，就可以得出氦丰度和HeIII区域开始的深度。可以用直接的\(\delta \nu_\mathrm{He}\)或者second difference frequencies\(\delta^2 \nu_{n,l} = \nu_{n+1,l} - 2\nu_{n,l} + \nu_{n-1,l}\)进行拟合，结果相差不大。
这两个频率差都会有一个长周期的量（大概是由其他原因引起的）、氦电离带来的项和对流层顶端带来的项，所以可以通过
\[\begin{align} \delta^2 \nu_{n,l} &= (a_1 + a_2\nu + \frac{a_3}{\nu^2}) + (b_1 + \frac{b_2}{\nu^2}) \sin{(4\pi\nu\tau_\mathrm{He}+ \phi_\mathrm{He})} + (c_1 + \frac{c_2}{\nu^2}) \sin{(4\pi\nu\tau_\mathrm{CZ}+ \phi_\mathrm{CZ})} \\ &= (a_1 + a_2\nu + a_3\nu^2) + (b_1 + \frac{\sin^2{(2\pi\nu\beta)}}{\nu\beta}) \sin{(4\pi\nu\tau_\mathrm{He}+ \phi_\mathrm{He})} + (c_1 + + c_2\nu + c_3\nu^2) \sin{(4\pi\nu\tau_\mathrm{CZ}+ \phi_\mathrm{CZ})} \end{align}\]来拟合里面的各种系数。
对模型的拟合
最容易尝试的当然是造一个模型和星震数据然后拟合看看是什么样子的。
dwarf拟合结果
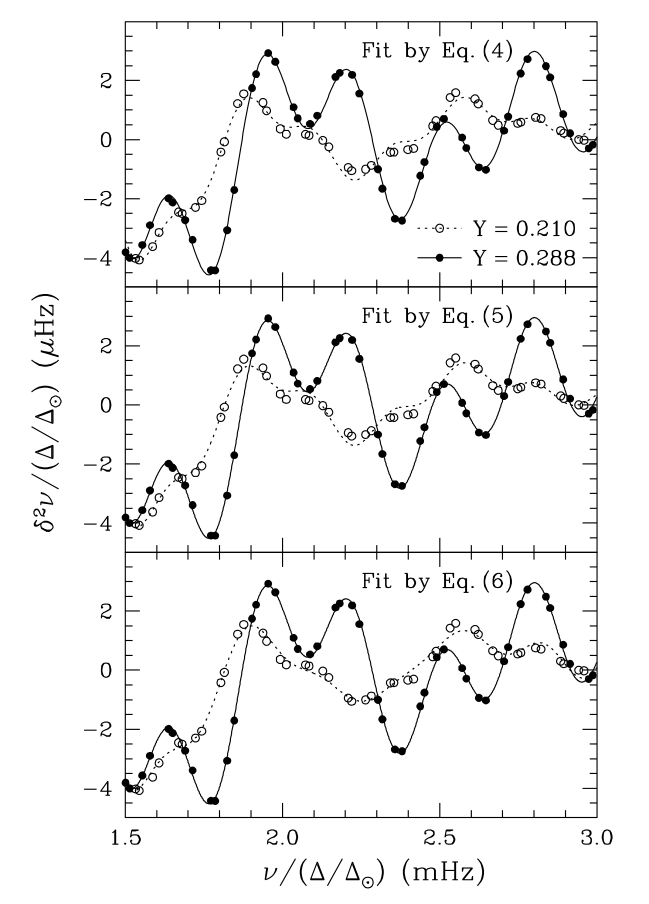Basu+04 Fig. 2
要注意的是恒星的密度（也就是\(M/R^3\)）对振动频率有scale，平均large frequency seperation对\(\delta^2 \nu_{n,l}\)的振幅有影响，需要改正（详见Basu+04, Section 2）。我们可以建立平均振幅(\(<A_\nu> = \frac{\int_{\nu_1}^{\nu_2} A_\mathrm{He}\nu e^{-8\pi^2\Delta_\mathrm{He}^2\nu^2} d\nu}{\int_{\nu_1}^{\nu_2}dv}\))和\(\tau_\mathrm{He}\)与\(Y\)的关系：
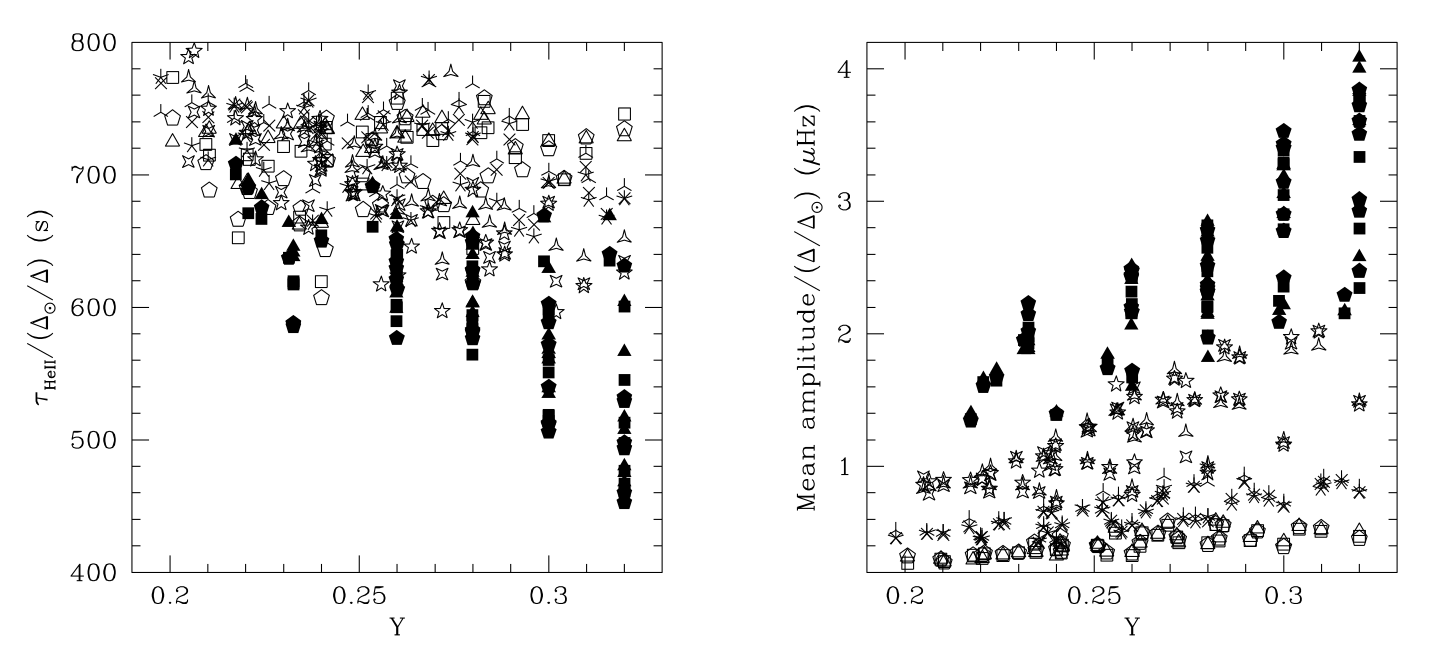Basu+04 Fig. 3
这俩都和氦丰度以及恒星质量有关。加上之前和密度的scale关系，如果我们知道质量或者半径的其中一个，那么拟合会准确很多，因为我们可以通过星震学数据得到它们的比例。其他的参数对振幅影响不大。
giant拟合结果
巨星的拟合结果比矮星的要差，因为很多矮星的p模在巨星中是混合模，所以用不了，能拟合的点就少了：
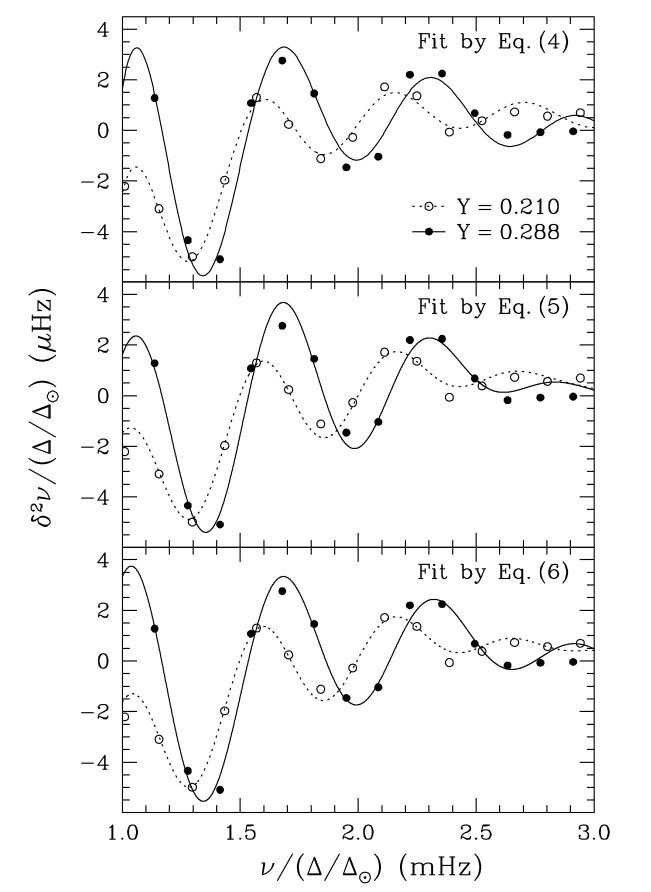Basu+04 Fig. 9
同时平均振幅还受金属丰度Z的影响很大。
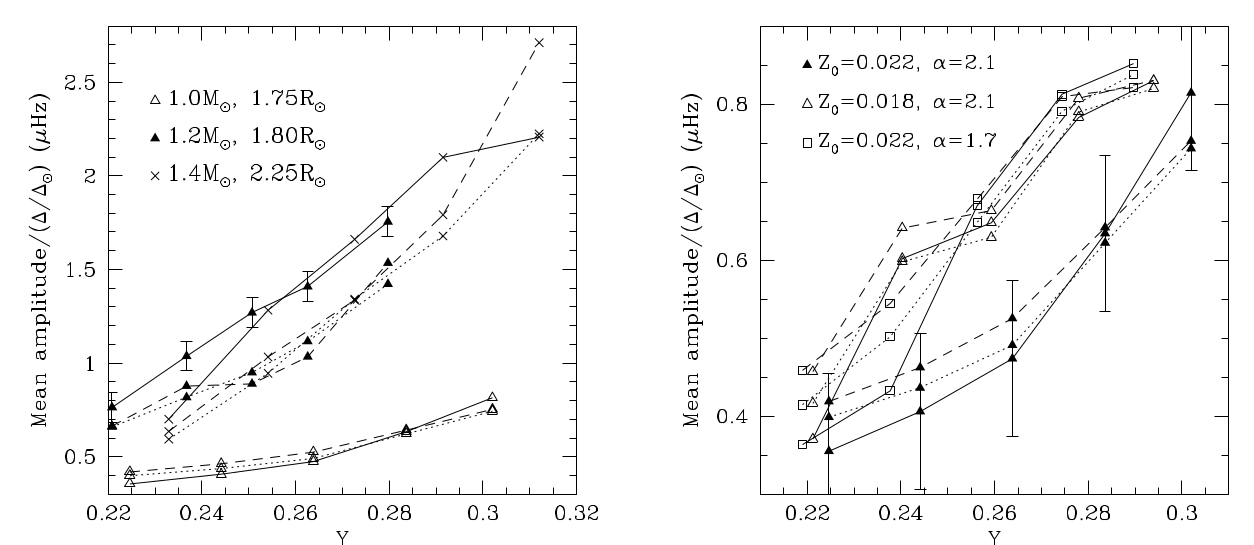Basu+04 Fig. 10
对巨星数据的拟合(Verma+19)
然后我们看看对数据的拟合是什么样子的。我们需要两个东西：类似于Basu+04 Fig. 10从模型中来的点以及关系、和实际测量的\(<A_\nu>\)。
对于第一个，我们可以用不同的质量、氦丰度、金属丰度、对流长、diffusion等参数产生一系列模型，再通过别的信息或者星震学信息限制其他的参数以得到只随氦丰度变化的模型，然后建立关系。第二个就测就是了。
结果证明，当质量小的时候测到的模数少，质量大的时候模的宽度太大，质量限制不好，所以只有1.0-1.3个太阳质量的星是不错的。同时对流是有必要的，但是大质量恒星的对流模型不好，所以它们的结果没有非对流模型好。大概就是质量适中的或者初始/表面氦丰度差小的可以用对流模型，其他的用非对流模型或者干脆别用比较好。模型的话还是用同一个模型去测同一个scale下的丰度比较好。
Verma+19给出了38颗Kepler矮星的氦丰度。McKeever+19给出了大概20颗疏散星团巨星的氦丰度。
