这玩意我从本科开始就没怎么搞懂（这数字哪来的？LPS这些又是什么鬼东西？）；还以为做光谱只需要用到别人做好的表格（拿来主义hhh），结果还是要搞懂。不然别人问起为什么这是三重态那是单重态我都说不出来。
复习一下：电子态
光谱项是描述原子的标识。而原子之间的区别实际上只在于电子所处的能级不同，所以光谱项说白了还是电子量子数的反映。
我们只需要四个量子数来描述电子，\(\boldsymbol{n}, \boldsymbol{l}, \boldsymbol{m}, \boldsymbol{s} \in \mathbb{Z}\)；主量子数、角量子数、磁量子数和自选量子数。\(\boldsymbol{n} \in [0, ...]\)，\(\boldsymbol{l} \in [0, ..., \boldsymbol{n}-1]\)，\(\boldsymbol{m} \in [-\boldsymbol{l}, ..., \boldsymbol{l}]\)，\(\boldsymbol{s} = \pm \frac{1}{2}\)。一个\(\boldsymbol{n}\)叫一个壳层，一个\(\boldsymbol{l}\)叫一个轨道，一个壳层一共可以容纳\(2n^2\)个电子。
麻烦的事情来了：我们用不同（但是会重复！）的字母来表示轨道和壳层。
| 主量子数\(\boldsymbol{n}\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 壳层名称 | K | L | M | N | O | P | Q |
| 角量子数\(\boldsymbol{l}\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 轨道名称 | s | p | d | f | g | h | i |
轨道鸣名称的前几个还是有来头的，其他的我不知道是怎么来的；总之这些名字增加了记忆的难度，好在它们大小写不同以及后面只会用到轨道名称，所以记住spd是012就可以了。
电子组态
原子里面可能不止有一个电子，那如何表示原子里面电子的状态呢？我们用电子组态来表示，也就是\(\boldsymbol{n}\)加上轨道名称。
比如说处于基态的氢原子电子为\(1s\)，被激发的氦原子可以为\(1s3p\)，某个处于激发态的氧原子电子组态为\(2s^22p^4\)；平方意味着有多少个电子处于这个态。我们能看出来电子组态只用了电子前两个量子数（我也不知道为什么不全部指明），所以一个电子组态有不止一种可能；比如\(sp^2\)有15种可能。这些可能性由泡利不相容原理，能量最低原则和Hund定则决定（所以不是20个）。
原子光谱项
只考虑LS耦合（因为研究的原子比较轻，原子序数小于40；如果重的话就要用jj耦合了），这个时候的好量子数是总轨道角动量\(\boldsymbol{L} = \sum{\boldsymbol{l}}_i\)、总自旋角动量\(\boldsymbol{S} = \sum{\boldsymbol{s}}_i\)和总角动量\(\boldsymbol{J} = \boldsymbol{L} + \boldsymbol{S}\)。 所以只要给定了原子中每个电子的\(\boldsymbol{l}, \boldsymbol{s}\)，就可以将这三个值定下来了。 前面两个都好说，\(\boldsymbol{S}\)的取值为\(\boldsymbol{J} \in [\boldsymbol{L}+\boldsymbol{S}, ..., |\boldsymbol{L}-\boldsymbol{S}|]\)。
有了这三个角动量量子数之后，我们就可以可以区分不同的原子状态了；定义如下的光谱支项：
\(^{2\boldsymbol{S}+1}L_\boldsymbol{J}\), \(\boldsymbol{n} ^{2\boldsymbol{S}+1}L_\boldsymbol{J}\), \(\boldsymbol{n} \boldsymbol{l}^x\) \(^{2\boldsymbol{S}+1}L_\boldsymbol{J}\)
三种写法都有，信息量依次增大；当然只有后两种才能完全区分光谱项。因为在原子物理里面多数时候是讨论原子最外层电子的激发，还有一种写法是只写出被激发电子的电子态。把\(\boldsymbol{J}\)省略掉的话就是光谱项了（求你写全好不好）。 这里的\(L\)是角动量量子数对应的轨道名称，也就是前面第二个表格的名称的大写。
实际上光谱项就是我们在能级图上看到的一条条横线，也是我们这么大费周章搞出这个东西的原因。
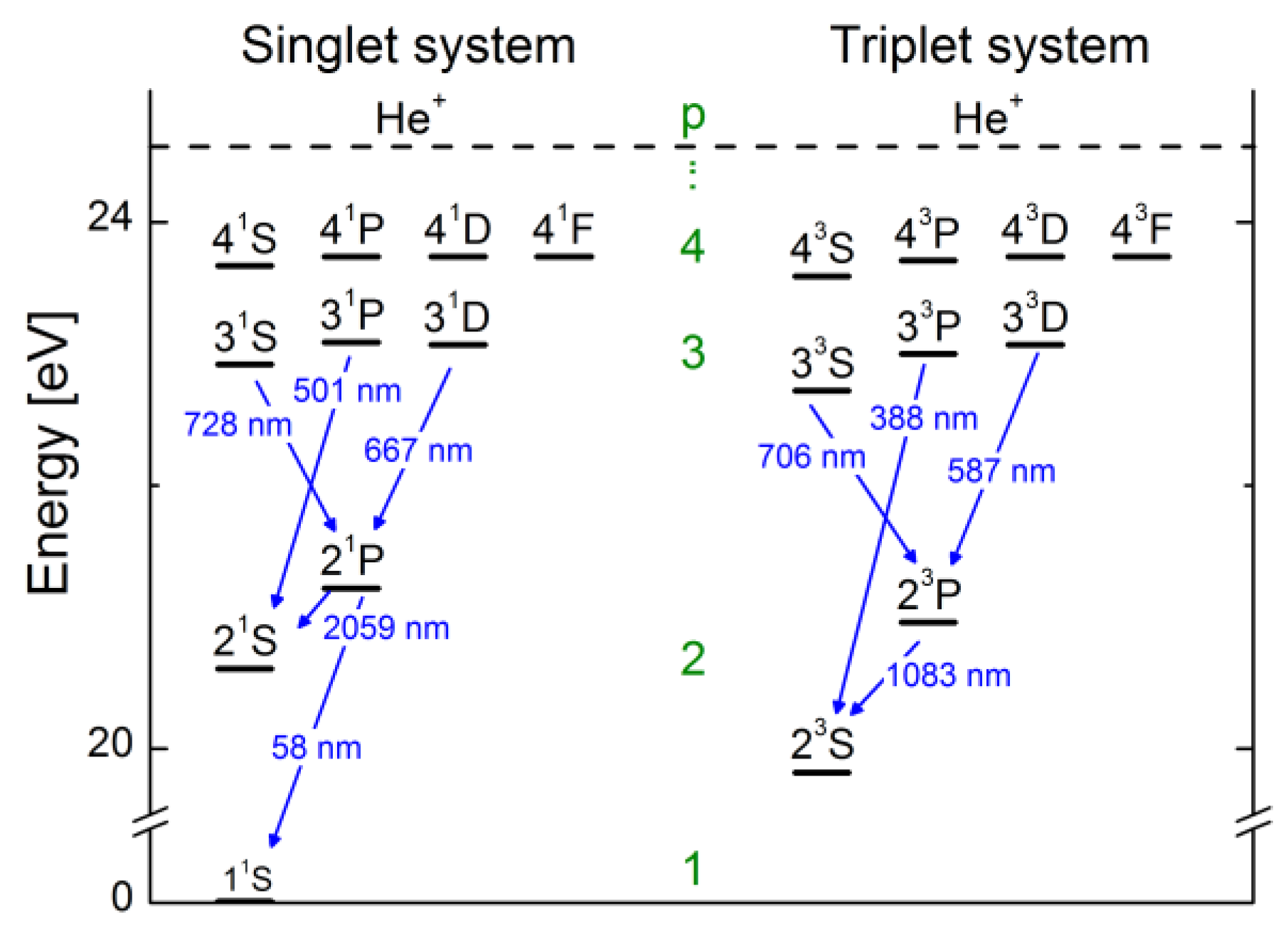credit:here
就我关心的He \(2^3\mathrm{S} \rightarrow 2^3\mathrm{P}\)跃迁来说，\(2^3\mathrm{S}\)的三个量子数分别为0, 1, 0，所以只有一个态（单重态），但是\(2^3\mathrm{P}\)可以有三个，\(2^3\mathrm{P}_0, 2^3\mathrm{P}_1, 2^3\mathrm{P}_2\)，所以这个跃迁有三条靠得很近的线。
至于它们具体怎么分布，那就不是我的事情了；找到了一个不错的网站，可以查询很多原子的能级分布，在这里
Ref
- http://www.astro.sunysb.edu/fwalter/AST341/qn.html
- https://www.nist.gov/pml/handbook-basic-atomic-spectroscopic-data
- https://www.gemini.edu/sciops/instruments/nearir-resources/
