又是比较简单的一章。而且因为连续谱一般和流量的绝对定标有关，我平常其实用得不多。
连续谱的确定主要能匹配出有效温度来，如果细节多一些的话\(\log{g}\)也可以确定。至于金属丰度就有点困难了，虽然也是有办法的。那么为了一次性地得到比较宽的光谱范围（毕竟高分辨率光谱需要更长的曝光时间，以及不同级数之间的流量定标相当麻烦），这里所说的连续谱的分辨率一般在10到15埃左右。在得到目标星光谱之后一般会有如下的流程：
- 比较目标星和标准星光谱
- 校准标准星光谱的形状
- 校准标准星某一个/某几个波长上的绝对流量
- 考虑谱线对目标星连续谱的影响
虽然书上是这么写，但是我觉得更好的顺序是2314，因为当考虑连续谱的绝对流量的时候没有校准好的标准星当然做不下去。
光谱仪
图片请参考第三章的图1。顺便从那里的\((3.15)\)可以得到
\[\Delta \lambda = -\cos{\alpha} \frac{W'd}{f_\mathrm{coll}n}\]因为分辨率不高，所以为了增加进光量一般会把狭缝开到比恒星的像更大。这个时候狭缝宽度将被星像的线宽度\(\Delta \phi F_\mathrm{eff}\)代替：
\[\Delta \lambda = -\cos{\alpha} \frac{F_\mathrm{eff}d}{f_\mathrm{coll}n}\Delta \phi \tag{10.1}\]由上式可以看到视宁度会影响光谱仪的分辨率，不过可以通过减小\(\frac{F_\mathrm{eff}}{f_\mathrm{coll}}\)来减小视宁度浮动的影响。
大气消光
当我们观测目标星和标准星的地平高度（或者说天顶距）不一样的时候，我们需要考虑大气消光的影响。当如下的情况：
- 平面平行层假设成立以及大气稳定
- 标准星不是变星
- 测得的有效波长不是天顶距的函数
成立时，就有最简单的流量与天顶距的关系：
\[F_\nu = F_\nu^0 e^{\tau_\nu \sec{Z}}\]\(F_\nu^0\)是大气层外的流量，\(\tau_\nu\)是恒星在天顶时大气层的光深。取个导数再把标准星加上：
\[\log{\frac{F_\nu(2)}{F_\nu{(1)}}} = \log{\frac{F_\nu^0(2)}{F_\nu^0{(1)}}} - \tau_\nu \log{e(\sec{Z_2}-\sec{Z_1})} \tag{10.3}\]当然天顶距越接近肯定越好，这也是高分辨率光谱在做天光改正的时候需要地平高度尽量相近的标准星的原因。假设的第3点不成立的情况一般是大气消光对某个波段的短波/长波影响比较大，导致了天顶距小的时候所有光都透了过来，天顶距大了之后就只能看见长波的光了。当然在相对较高的分辨率下（小于50埃），这个问题基本不需要考虑。
标准星的校准
标准星在不同波段的流量先相对于5556埃校准，然后我们再校准5556埃的绝对流量。标准星一般是织女星或者太阳。
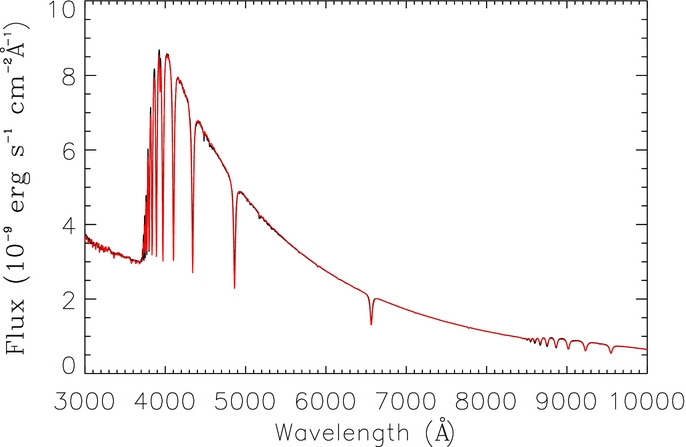织女星的光谱
上面的其实已经不只是连续谱，而是高分辨率光谱了。以前的低分辨率光谱在大于8500埃那里会有很大的弥散，就是因为Pashen线系的存在。
要多说几句的是这种图横纵轴的单位是比较容易混淆的。光谱的话，我们关心的是每个波长/频率上的流量是多少，所以\(\lambda\)要和\(F_\lambda\)对应，\(\nu\)要和\(F_\nu\)对应。而SED的话，则是每个波长/频率上的能量是多少，所以纵轴要相应地变为\(\lambda F_\lambda\)和\(\nu F_\nu\)。取\(\log{}\)之后可以把流量/能量比较低的部分的差异放大，但是单位就没有了。
其他的校准和杂七杂八的东西
谱线带来的吸收可以用模型或者高分辨率光谱来改正。有的时候为了确定一些物理量，我们会比较关注连续谱的斜率以及氢线系的线系限，但是光学的Balmer线系限除了有跳跃之外还有非常多的Balmer线，模糊了线系限左右的流量。所以有必要的话需要增加紫外/红外的观测。
校准好之后将光谱和模型比较就可以得到恒星参数了。
热星等
略。
