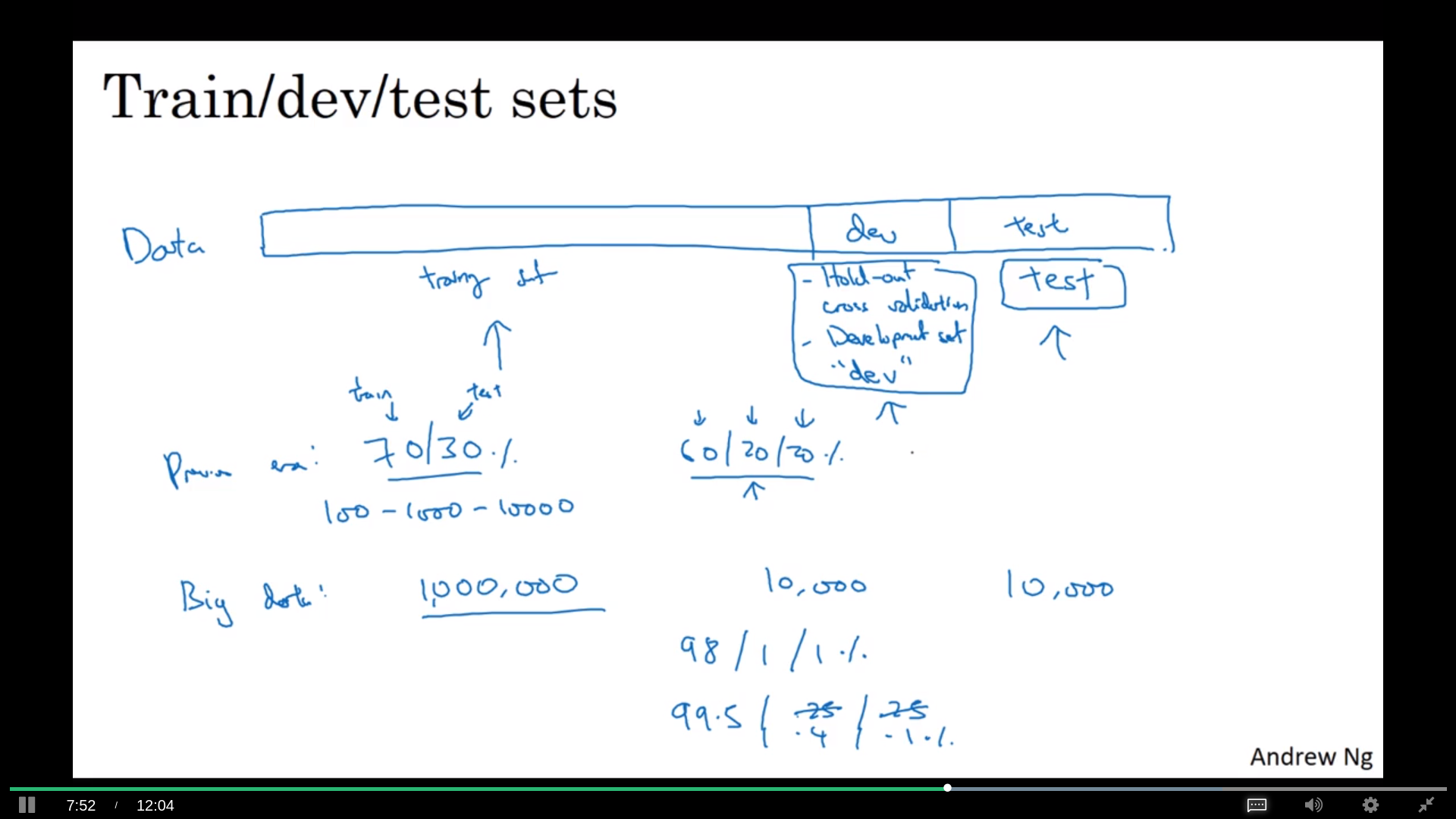
数据集
以前是分成两个的,训练和测试。现在分成3个,训练、发展和测试集。用发展去测试训练,最后再用测试去测试表现;甚至没有测试集都行。这里的区别是发展集是用来overfitting的,测试集不是。
要注意不同数据集的数据要同质,质量相同
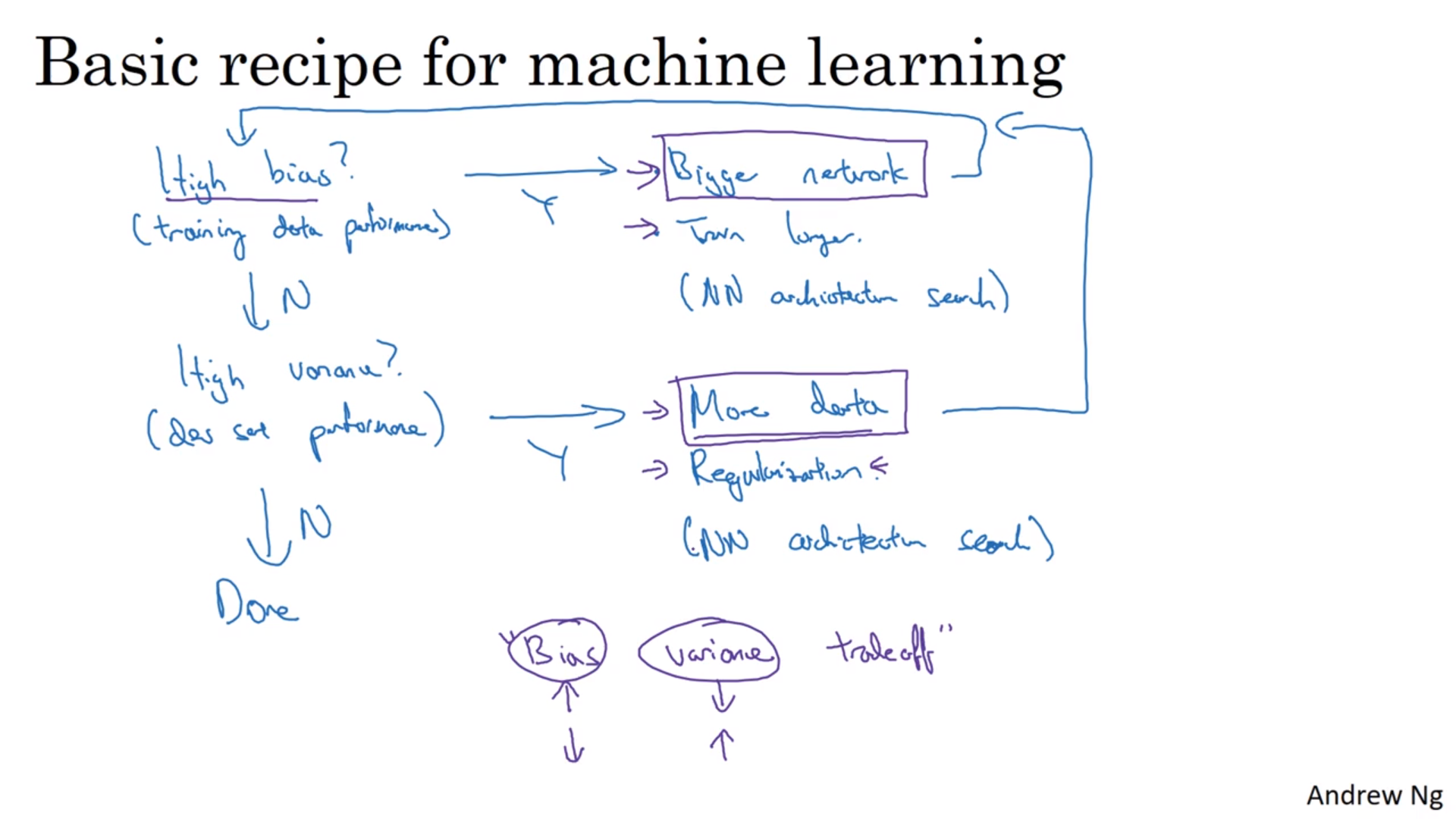
bias和variance
训练集的错误率比与预期的高:高bias;发展集的错误率比训练集的高:高variance

正则化
在代价函数后面加上\(w\)的2或者1范数
通过强制减小\(w\)简化神经网络,减小权重。


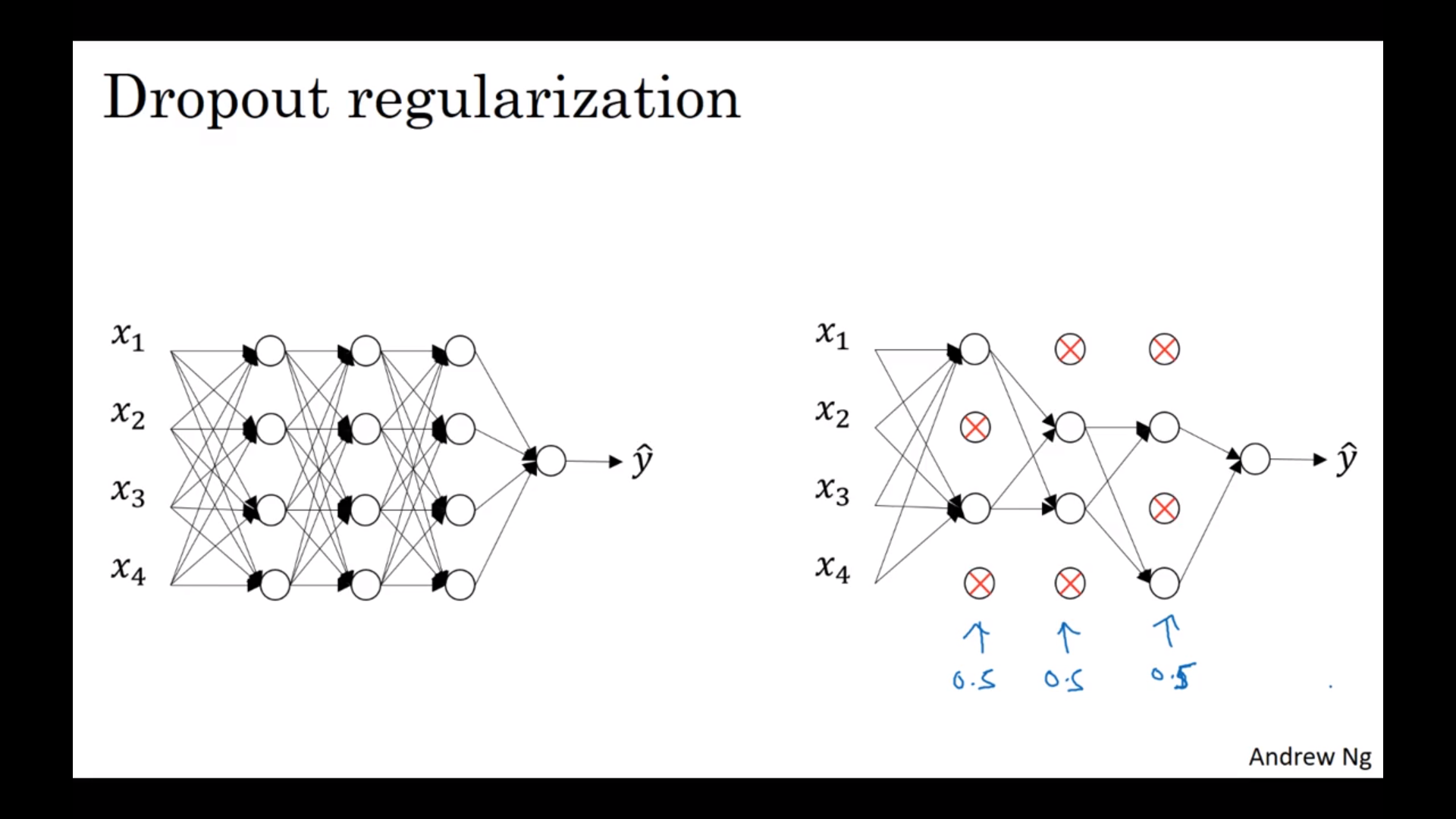
Dropout正则化
随机删掉一些节点来做一次正反向传递,然后不断重复。要注意的是删掉之后要把整个节点的值除以一个删掉的阈值概率,把取值回覆到正常水平。测试集不要用。Dropoyt的意思是不让某个节点依赖于某几个前面一层的节点,所以也是减小权重的意思。不同的层可以有不同的dropout节点数。输入层一般不dropout(或者是很小的duopout数)。最后在看J减小的时候要小心一点,必要的时候关掉dropout
奇技淫巧
增加训练样本:把图像翻过来/旋转/放大,或者几种加起来。不过信息量其实还是一样的。标准是人脑还是会把它当成同一样东西。
提早停止:看发展集的误差,以它的最小值为基准。思路是\(w\)会随着迭代而不断增大,导致太大以至于我们不想看到。提早停止可以防止这个。
正交化:将减小损失函数和防止overfit分开。提早停止违反了这个原则。
L2正则化比较简单,不过要试各种的\(\lambda\)。
建立最优化问题
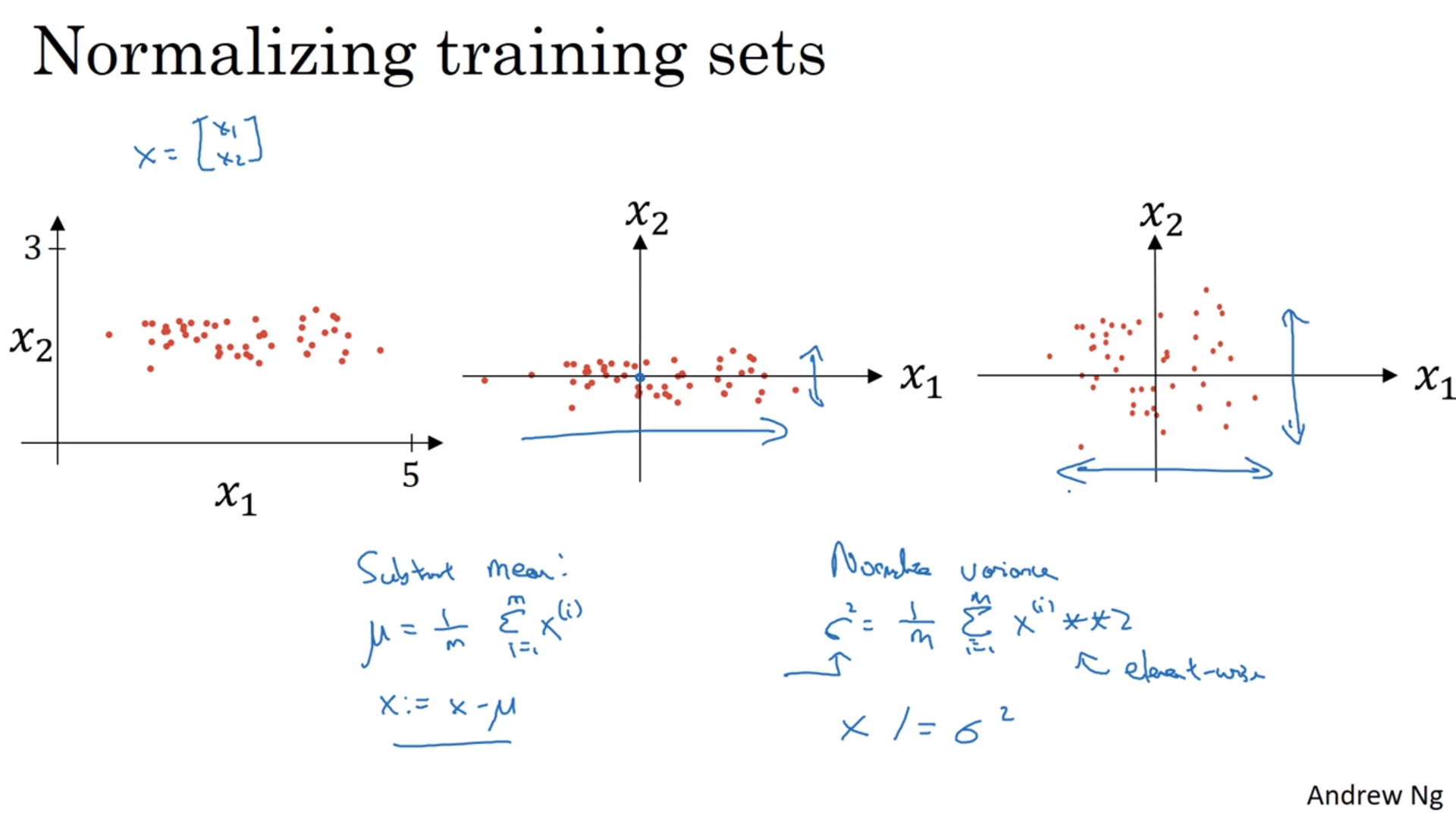
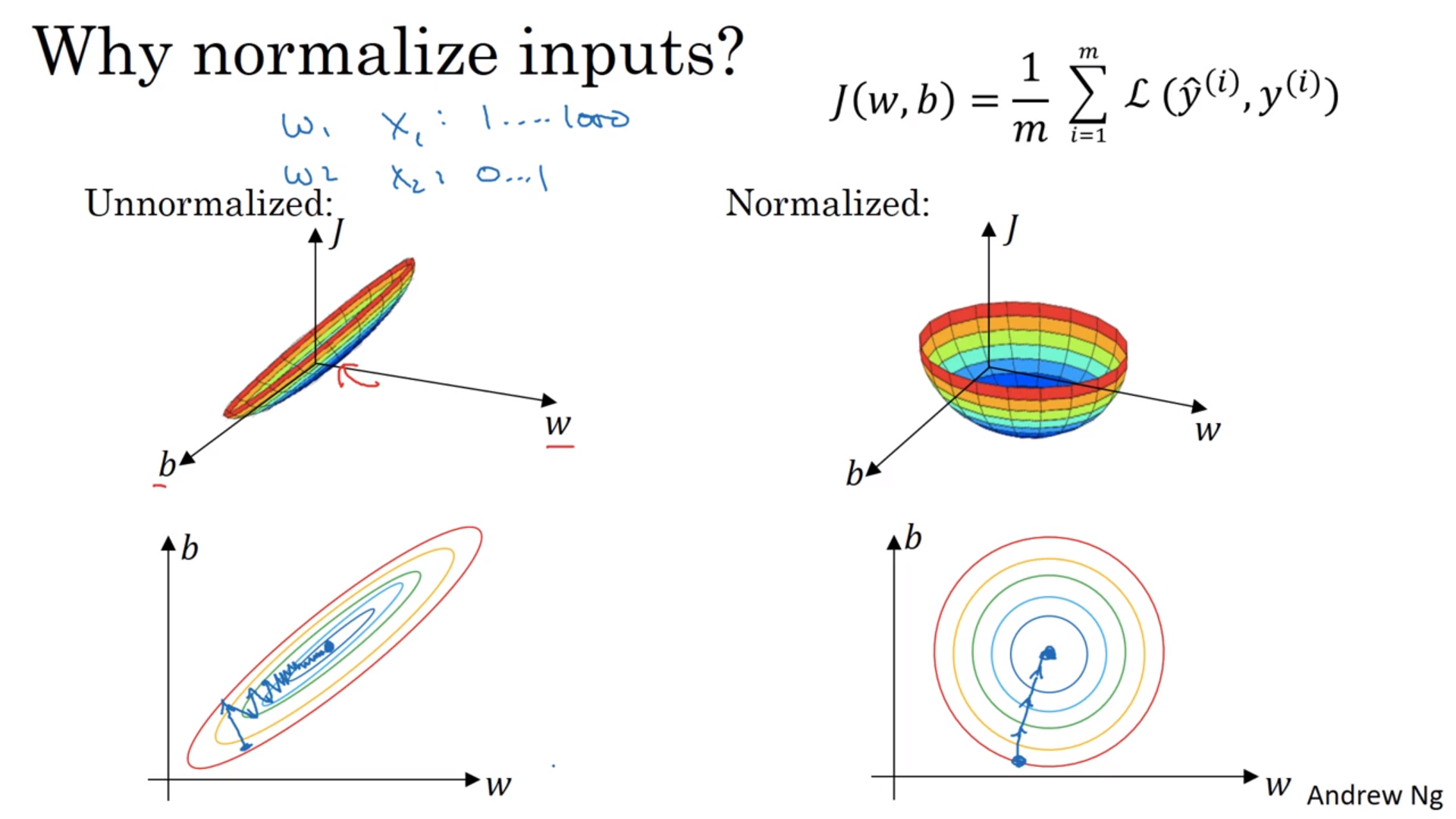
归一化训练集
看图,把输入数字移到0左右,将标准差scale到1。注意训练集和测试集的移动和scale需要完全一样。
这么做的理由:将代价函数搞得好看一点,简单一点,学习速率也能快一点。
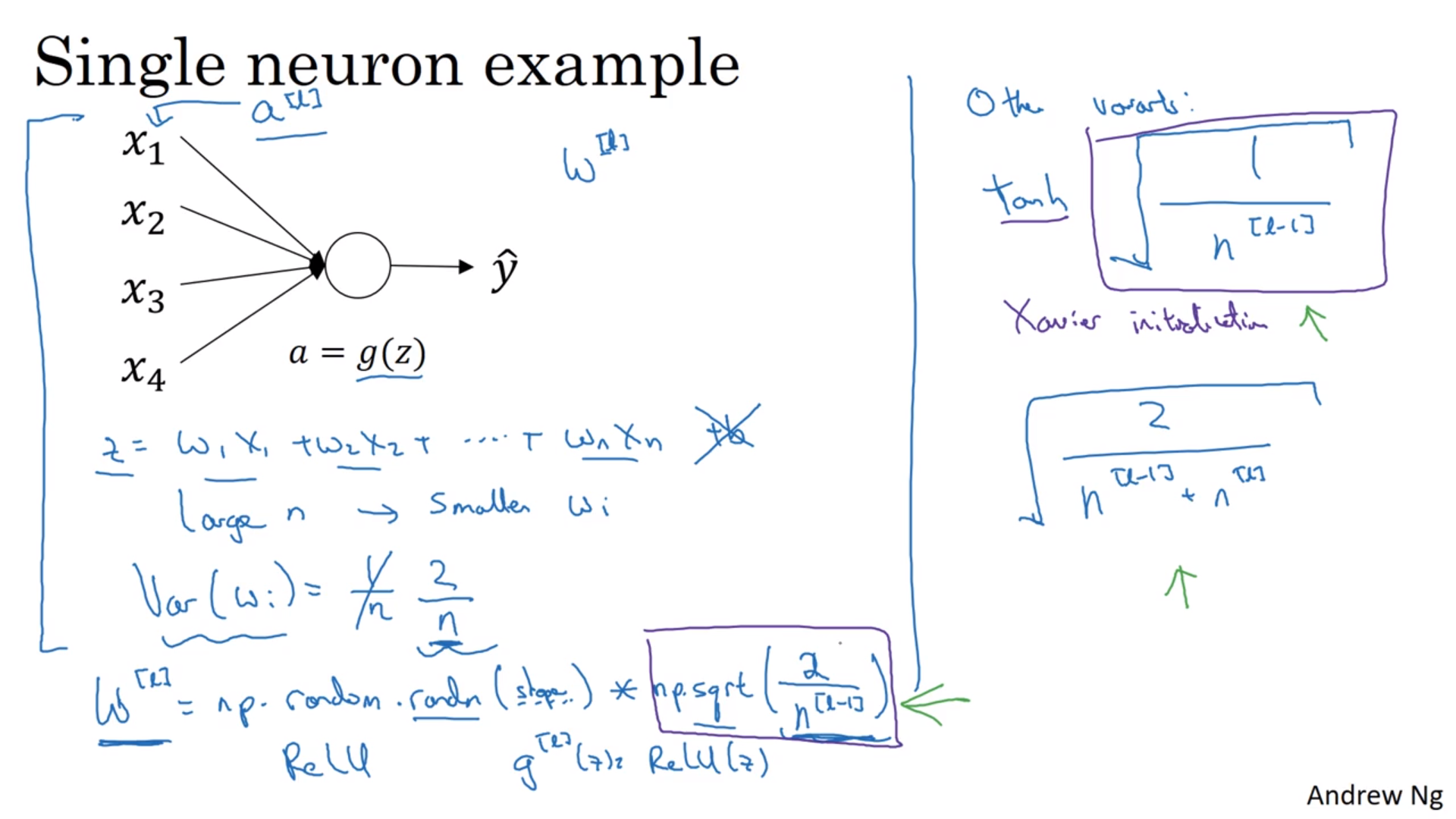
奇怪的导数值
在训练很深的神经网络的时候,有的时候导数值可能会很大或者很小,比如矩阵遇到了指数增长/减小什么的。
一个治标的办法是选择初始的权重。\(z = w_1x_1 + w_2x_2 + \cdots + w_nx_n\)。\(n\)越大,\(z\)就越大,所以我们控制\(w\)的标准差为\(\sqrt{\frac{2}{n^{[l-1]}}}\)。这里的2是Relu函数带来的。当然也可以当它是一个超参数来试。
导数值检查
往左和往右挪,计算\(\frac{y}{x}\)。愣算就行。
具体:将所有的参数竖着排成一个巨长的向量,包括正向的和反向的。然后愣算其中某个参数的导数,看两个向量之间的二范数比各自的二范数的大小。比值是拿来看相对大小的,防止它们本来就很小或者大。
检查只能用在debug上。如果出错了,看具体的值哪个不正常。如果有的话,记得加上正则化项。检查不能用在dropout上,要用的话先关掉。

加速
切成小块
每次只处理1000个训练样本,然后循环。基本上都得用。计算1000个之后就马上更新参数。当然也可以见到1个,不过随机性就很强;这也被叫做随机梯度下降。随机梯度下降相当于没有向量化,所以很慢,而且很多噪音。
但是怎么选小块的大小?当整体训练样本小的时候,当然应该整个一起搞;如果大的话,可以用2的某次方来做(可能快一点),或者和CPU/GPU匹配的大小。试呗。
不用梯度下降
指数平均
其实就是滑动平均的一种,只不过前后的数据不平权。
\[v_t = \beta v_{t-1} + (1-\beta)\theta_t\]它会将之前的数据累积起来,但是不断乘上\(\beta\)。大概相当于前\(\frac{1}{1-\beta}\)天的温度平均:\(v_t = \sum_{i=0}^n 0.1 \times 0.9^i \theta_i\)。
Bias Correction
更准确的计算。因为上式从0开始,所以一开始的时候肯定是不对的。当然一般数据量大的话可以不管,反正可以等。或者除一个\((1-\beta^t)\)。
Gradient descent with momentum
\[\begin{align} v_{dW} &= \beta v_{dW} + (1-\beta) dW \\ v_{db} &= \beta v_{db} + (1-\beta) db \\ W &= W - \alpha v_{dW} \\ b &= b - \alpha v_{db} \\ \end{align}\]这样做的好处是它会在摆动的方向将摆动平均掉,在正确的方向保留导数值,所以可以加速收敛。一般\(\beta = 0.9\)是个不错的选择。
RMSprop
另一种方式的加速。看图。
Adam
合在一起。看图。
降低学习速率
可以手动降低,乘上一个线性增大的分母,或者是e指数减小
避免局部极小
很多导数为0的点实际上是鞍点,因为参数非常多。不过在那附近会转悠好久,比较慢。
调超参
要调的东西
学习速率\(\alpha\);动量项\(\beta / (\beta_1=0.9, \beta_2=0.999, \epsilon=10^{-8})\)、多少节点、mini-batch大小;多少隐层、学习速率变化。
但是调超参的时候不要用网格,随即就好;因为超参数量太多了,而且不同的超参对模型影响不同,所以随机会给所有的超参更多选择。最初的参数空间可能比较大,都跑一次之后可以缩小参数空间再做一次。随机的时候,对于某些超参,也可以不用平均随机,而是用其他的概率分布,或者log scale,量级上平均就行。或者说在模型对超参变化更剧烈的时候放更多的点。
训练中
训练中可以不断调整超参什么的。或者同时训练很多个模型,有钱有资源的话。
让模型更稳健
逻辑回归的时候将输入归一化可以让代价函数更规则,那么在神经网络里面也可以这么做,对\(z\)归一化。可以将\(z\)的平均值和标准差倒过来,或者自己设定一组数,或者让网络自己学习去。\(b\)也可以不要了,因为归一化的时候带上了常数。
其他具体流程和普通的差不多。它防止了隐层的值的分布距离原点太远。它会带来一些噪声。
在测试集的时候,我们可以用指数平均的方法记录训练集的平均值和scatter,然后当成测试集的均值以及\(\sigma\)。
多项选择题
Softmax回归。在最后一层隐层的地方将节点数和分类数相等,让每一个节点表示属于每一类的概率。sigmod函数会变成softmax函数,对这节点的值进行e指数,归一化。因为e指数会将值之间的差异扩大,所以可以进行分类。如果只有两类的话,softmax会退化回逻辑回归。
损失函数:
\[L(y, \hat{y}) = -\sum y_j \ln{\hat{y_j}}\]只留下正确的那一项,然后最大化它的概率。
代价函数:还是损失函数的平均。
反向传递:
\[dz^{[l]} = \hat{y} - y\]但是在用框架的时候,只要正向传递对了,反向传递交给框架就行。
机器学习框架
易用、快速、开源(特别是长期开源)