逻辑回归
Binary Classification
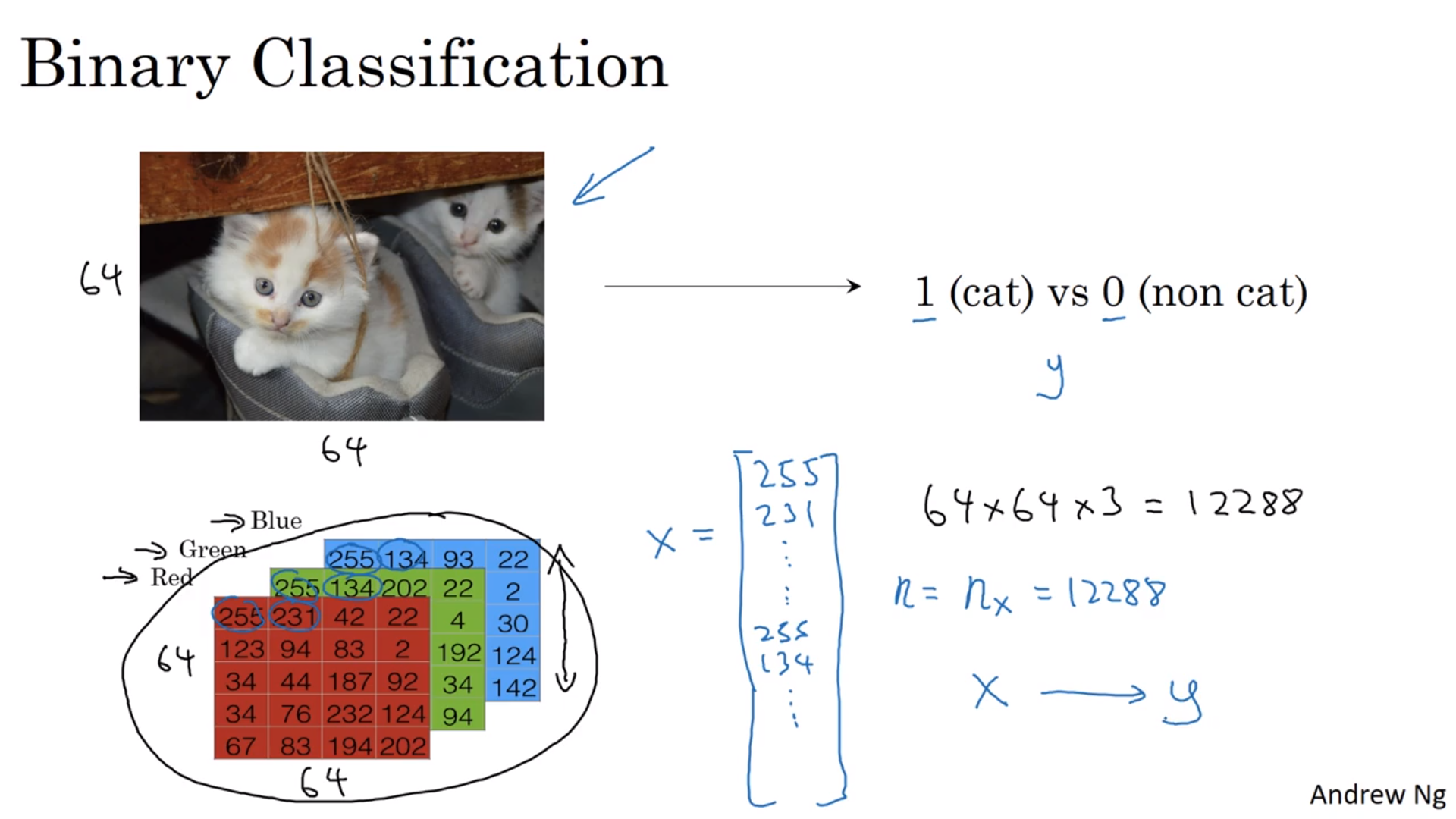
Binary Classification指的是输入一堆东西,最后给出一个只有两个结果(0或者1)的输出的分类过程。一个典型而符合惯例的例子是判断某张图片上有没有猫,也就是将图片的红绿蓝像素值矩阵作为输入,是猫(1)以及不是猫(0)作为输出。
在这里我们不考虑这么多细节,直接将红绿蓝的像素排成一列,作为输入\(x\)。\(x\)的大小就是总的像素数\(n_x\)或者\(n\)。
如果按照位置来排呢?
需要在开始之前明确一些记号。
我们在寻找解的时候的输入为\((x, y)\),当然就是\((图片, 是否猫)\)的组合了。其中\(x\)是一个\(n_x\)行的列向量,即\(x \in \mathbb{R}^{n_x}\);而\(y \in \{0, 1\}\)。当然这只是一个样本,而我们一般会有很多的训练样本(training set):\(\{ (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), ..., (x^{(m)}, y^{(m)}) \}\)。\(m\)即为训练样本的数量;当我们需要明确的时候我们会把训练样本数和检验样本(test set)数写成\(m_\mathrm{train}, m_\mathrm{test}\)。
这么写当然比较麻烦,所以我们有矩阵写法。首先将所有的\(x\)排成一行,就成了一个\(n_x\)行\(m\)列的矩阵\(\boldsymbol{X}\)。数学语言表达就是\(\boldsymbol{X} \in \mathbb{R}^{n_x\times m}\),python表达就是X.shape = (nx, m)。把\(\boldsymbol{X}\)转置也不是不行,不过会比较麻烦,就不用了。
相应的所有的label也这么排,就成了一个一行\(m\)列的“矩阵”\(\boldsymbol{Y} = [y^{(1)}, y^{(2)}, ..., y^{(m)}]\);或者说\(\boldsymbol{Y} \in \mathbb{R}^{1\times m}\),Y.shape = (1, m)。
更多的记号可参阅课程给的pdf。

逻辑回归
实际上逻辑回归是在二项分布之下的一个概念,是实现二项分布的一个方法。我们需要的是在上面的定义下,构造一个盒子,接收输入\(x\), 并输出在输入\(\mathbf{x}\)的情况下二项分布结果为1的概率\(\hat{y} = P(y=1 \lvert \boldsymbol{x})\)。然后我们有相应的参数\(\boldsymbol{w} \in \mathbb{R}^{n_x}, b \in \mathbb{R}\)。
构造输出\(\hat{y}\)的第一反应应该是
\[\hat{y} = \boldsymbol{w}^\mathrm{T} \boldsymbol{x} + b\]这其实就是普通的线性回归。但是我们要求\(\hat{y}\)是一个概率,取值在0到1之间,而线性回归不仅不能保证结果小于1还会出现负的结果,当然是不对的。
那怎么办?很简单,给线性回归的结果套一个值域在0到1之间的函数不就行了呗。这种函数一般都跟\(e\)指数有关,所以我们有sigmod函数:
\[\sigma(z) = \frac{1}{1+e^{-z}}\]图像请看截图的左下角。
有了sigmod函数之后,只要令
\[\hat{y} = \sigma(\boldsymbol{w}^\mathrm{T} \boldsymbol{x} + b)\]就行了。加上了sigmod函数之后的回归就叫逻辑回归。有的方法把\(b\)也放进\(\boldsymbol{w}\)里面,不过这里不这么做。
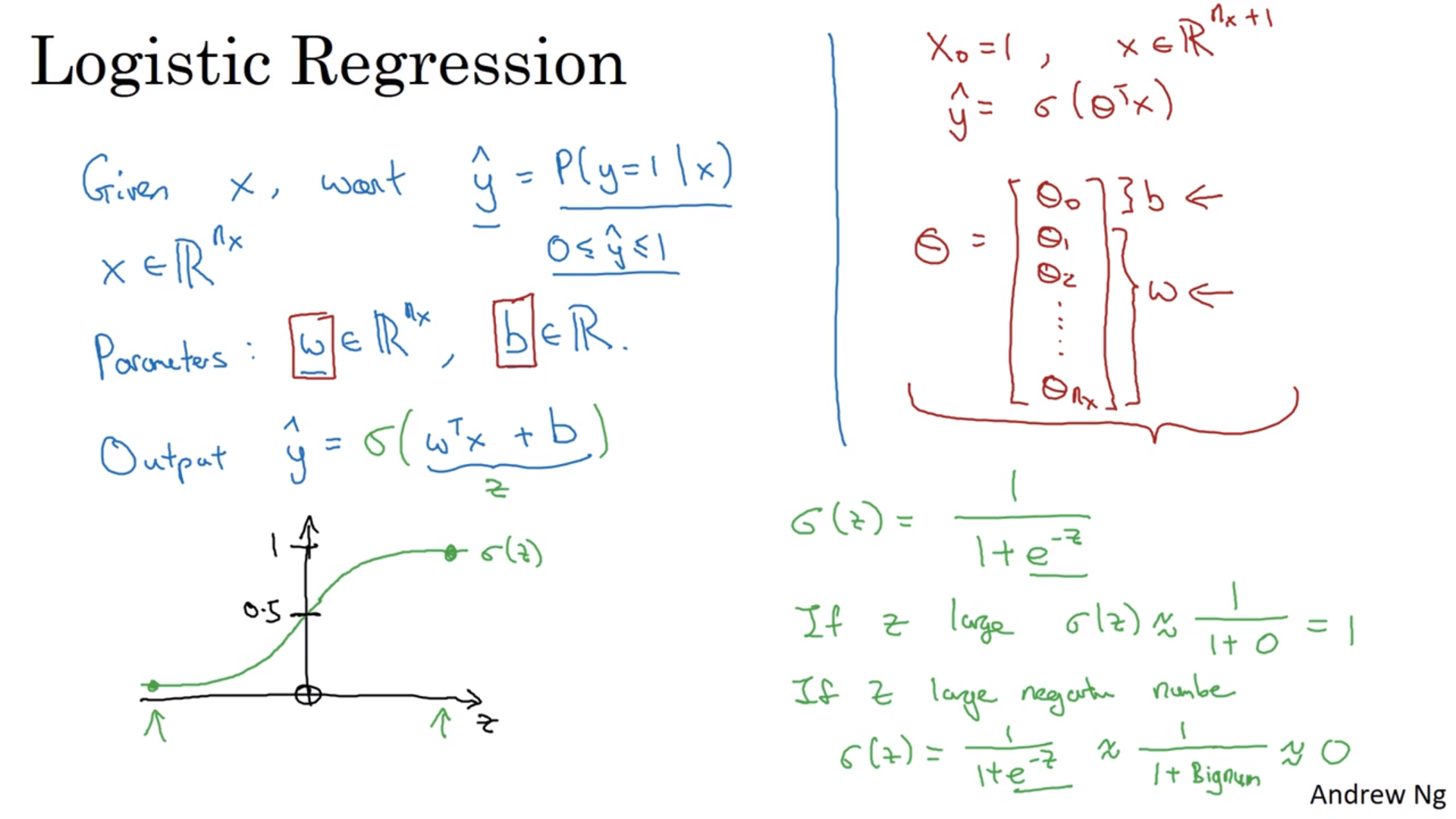
代价/损失函数
代价/损失函数就是用来训练上面提到的\(\boldsymbol{w}, b\)的。这个函数越小,模型的效果越好(对于训练样本来说)。这里定义的损失函数只是对于一个训练样本来说的,而代价函数是对于整个训练样本集在某一堆参数下的评价。
学过线性拟合的同学们马上又该反应过来,一个典型的代价函数就是\(L(\hat{y}, y) = (\hat{y} - y)^2\)。但是这个函数的效果并不好,所以我们实际上用的是这个:
\[L(\hat{y}, y) = -[y \ln{\hat{y}} + (1-y) \ln{(1-\hat{y})}]\]大致地说为什么代价函数的样子是这样的原因是,差值的平方会导致函数非凸,但是上面的定义加上sigmod函数会使得\(L\)是个凸函数,没有局部极值。
对应的代价函数我们选择这个:
\[\begin{align} J(\boldsymbol{w}, b) &= \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)}, y^{(i)}) \\ &= - \frac{1}{m} \sum_{i=1}^{m} [y \ln{\hat{y}} + (1-y) \ln{(1-\hat{y})}] \end{align}\]只要找到最小化\(\boldsymbol{w}, b\)的\(J\),就行了。实际上逻辑回归就是一个小型的(可能还是最简单的)神经网络。

如何训练参数?
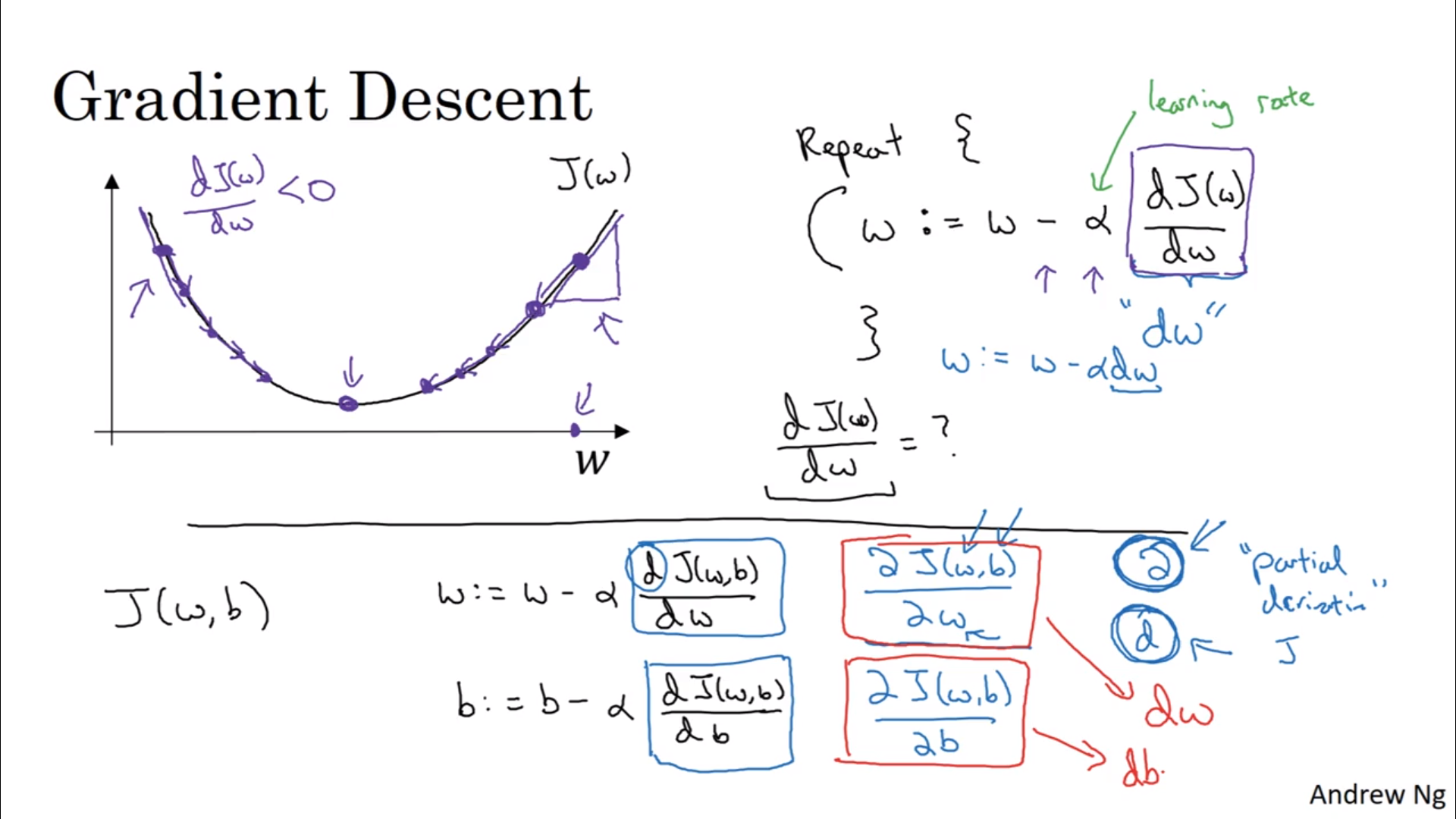
最小化\(\boldsymbol{w}, b\)就是在\(J(\boldsymbol{w}, b)\)这个表面上(简单来说)迭代地找到这个函数的最小值以及对应的参数。又该反应过来我们需要用到导数来指导我们向哪里走了。具体来说,是计算这个:
\[\begin{align} \boldsymbol{w} &:= \boldsymbol{w} - \alpha \frac{\partial J}{\partial \boldsymbol{w}}\\ b &:= b - \alpha \frac{\partial J}{\partial b} \end{align}\]\(\alpha\)被称为学习速率,是人选的;而后面的俩偏导数是需要计算的,在python中会被命名为dw, db。
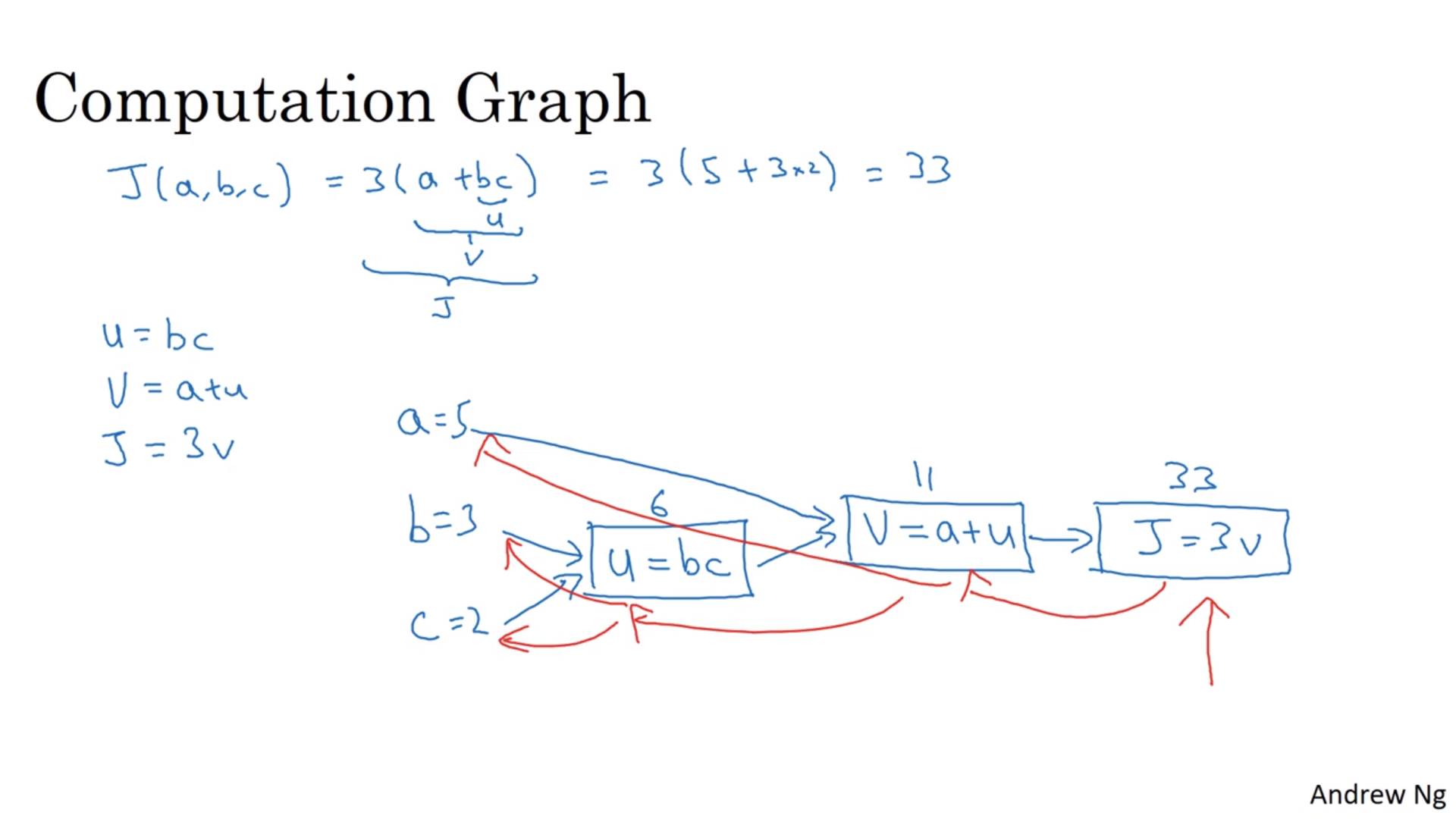
正反向传递
具体请看截图。正向传递的意思是从具体参数计算代价函数值的过程(蓝色、从左到右),而反向传递指的是计算导数的过程(红色、从右到左)。
导数的具体计算
我们举一个简单的例子:
\[\begin{align} z &= w_1 x_1 + w_2 x_2 + b \\ \hat{y} &= \sigma(z) \\ L(\hat{y}, y) &= -[y \ln{\hat{y}} + (1-y) \ln{(1-\hat{y})}] \\ \end{align}\]自然地
\[\begin{align} \frac{dL}{d\hat{y}} &= -\frac{y}{\hat{y}} + \frac{1-y}{1-\hat{y}} \\ \frac{d\hat{y}}{dz} &= \hat{y} (1-\hat{y}) = \sigma (1-\sigma) = \hat{y} - y \\ \frac{dz}{dw_1} &= x_1 \frac{d\hat{y}}{dz} \\ \frac{dz}{dw_2} &= x_2 \frac{d\hat{y}}{dz} \\ \frac{dz}{db} &= \frac{d\hat{y}}{dz} \\ \end{align}\]在代码中我们基本上会用导数的分母作为变量名字。

之后我们需要算的就是代价函数了。其实也没什么,就拿一个变量做代表吧:
\[\frac{\partial J}{\partial w_1} = \frac{1}{m} \sum_{i=1}^{m} \frac{L^{(i)}}{\partial w_1}\]具体的计算过程就是一个正向+反向传递的过程:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 设置初值
J = 0; dw1 = 0; ...; db = 0
for i in np.arange(1,m+1):
# Forward propagation
z[i] = w.T * x[i] + b
a[i] = sigmod(z[i])
J += L(a[i], y[i])
# Backward propagation
dz[i] = a[i] - y[i]
dw1 += x1[i]dz[i]
...
db += dz[i]
J /= m; dw1 /= m; ...; db /= m
w1 = w1 - alpha * dw1
...
b = b - alpha * db
然后继续迭代。所以“正常”情况下要用两个循环嵌套,显然是不现实的,所以要用到python的向量来做。
向量化
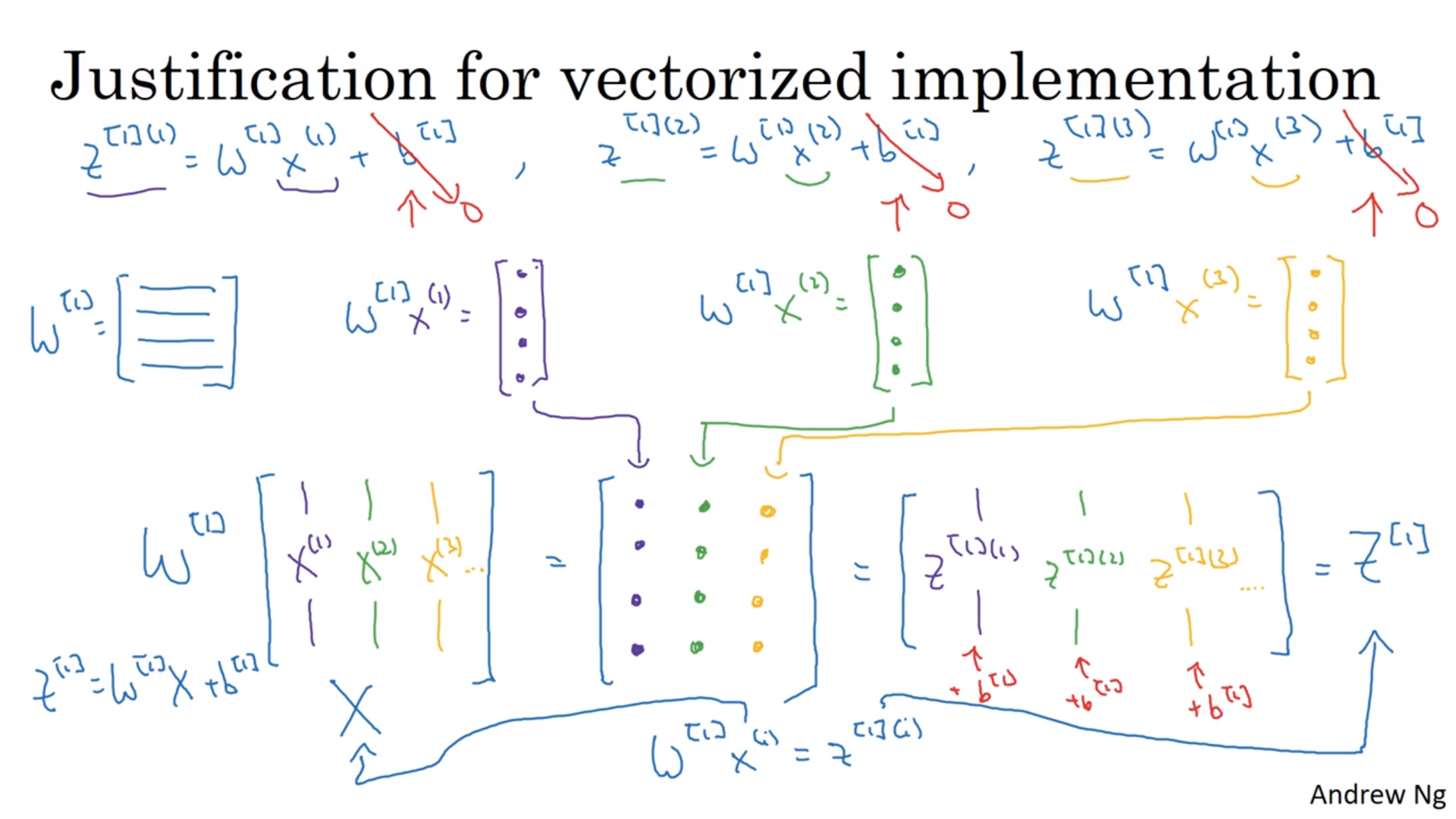
当w是一个列向量的时候,比如要算z[i] = w.T * x[i] + b的时候,可以这么做:np.dot(w,x)+b。高级一点的话直接和矩阵相乘:np.dot(w,X)+b。
dz[i] = a[i] - y[i]可以转为dZ = A - Y;dw1 += x1[i]dz[i] -> dW = 1/m * X*dZ.T;db += dz[i] -> 1/m * np.sum(dZ)。还要注意的一点是在reshape的时候最好把行列都写全。
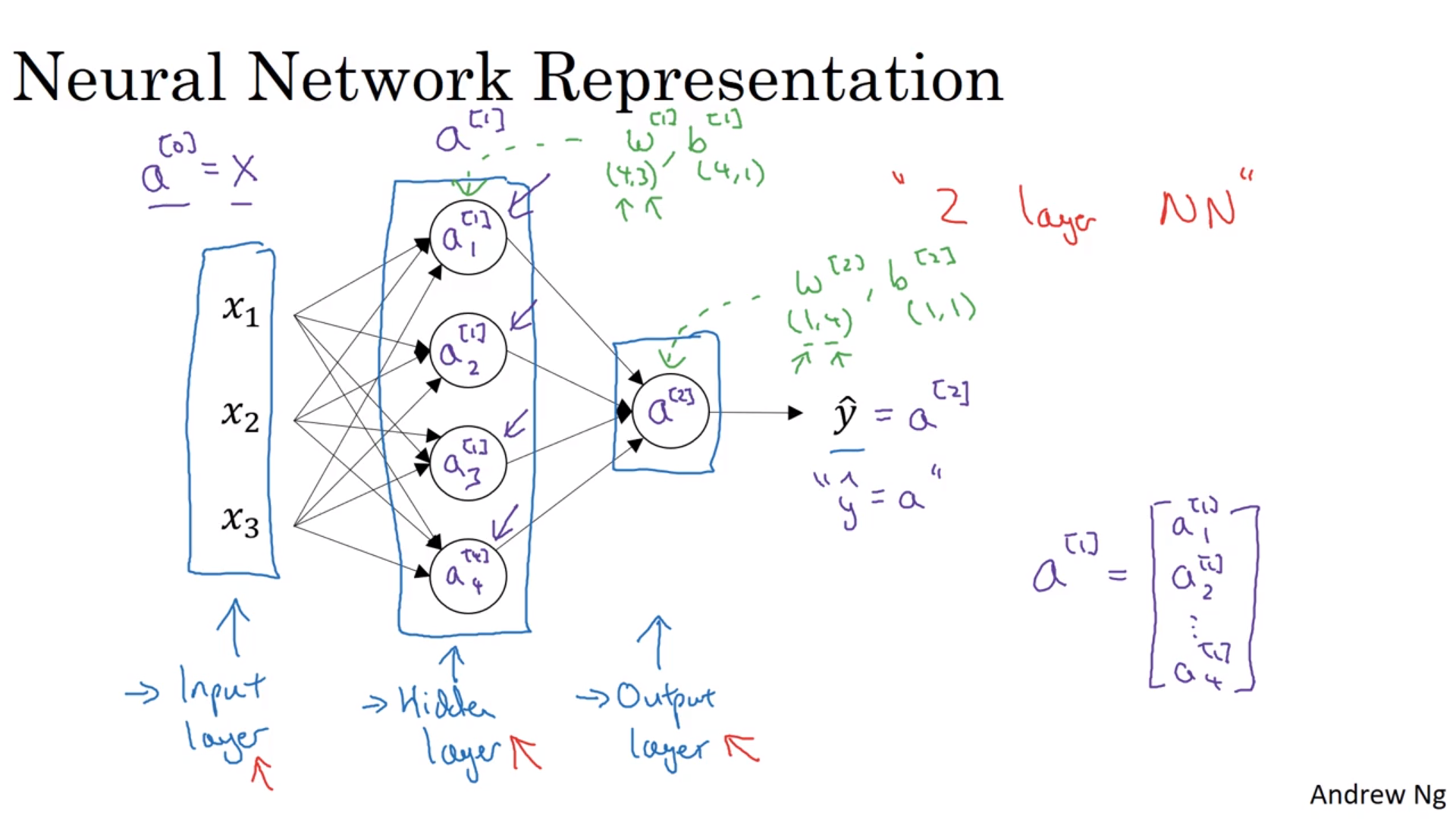
浅神经网络
[1],[2]代表神经网络的层数;(i)代表某一个训练样本(都是上标)。下标不带任何括号,表示某一层中的第几个节点。当有两层的时候,刚开始的输入是\(x\),但是之后的输入会变成了\(a^{[i]}\)这样。
神经网络的命名
输入层、隐层、输出层。\(a^{[0]} = x\)。在数层数的时候,不算输入层。每一层都有一套\(w, b\)配套。
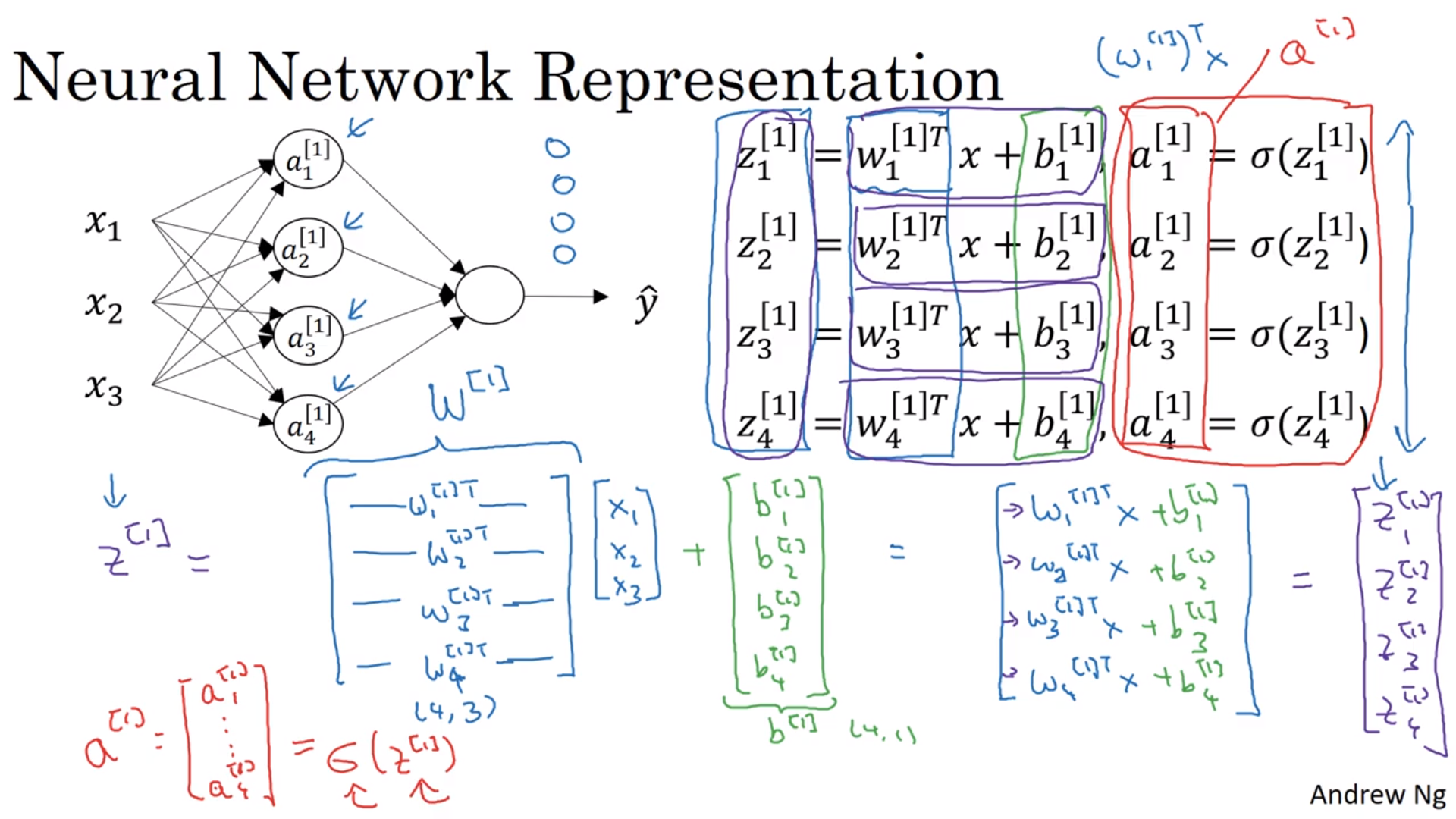
每一个节点都有两步:线性回归以及丢进sigmod函数里面。所以都有两条公式:
\[\begin{align} z_1^{[1]} &= w_1^{[1]T}x + b_1^{[1]}, a_1^{[1]} = \sigma(z_1^{[1]}) \\ z_2^{[1]} &= w_2^{[1]T}x + b_2^{[1]}, a_2^{[1]} = \sigma(z_2^{[1]}) \\ z_3^{[1]} &= w_3^{[1]T}x + b_3^{[1]}, a_3^{[1]} = \sigma(z_3^{[1]}) \\ z_4^{[1]} &= w_4^{[1]T}x + b_4^{[1]}, a_4^{[1]} = \sigma(z_4^{[1]}) \\ \vdots \end{align}\]能看到这些式子排得很整齐,那何不矩阵化了呢?
\[z^{[1]} = \begin{bmatrix} z_1^{[1]} \\ z_2^{[1]} \\ z_3^{[1]} \\ z_4^{[1]} \end{bmatrix} = \begin{bmatrix} \cdots w_1^{[1]T} \cdots \\ \cdots w_2^{[1]T} \cdots \\ \cdots w_3^{[1]T} \cdots \\ \cdots w_4^{[1]T} \cdots \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} + \begin{bmatrix} b_1^{[1]} \\ b_2^{[1]} \\ b_3^{[1]} \\ b_4^{[1]} \end{bmatrix} = W^{[1]} x + b^{[1]}\]\(W^{[i]}\)是一个\(n^{[i]}\)(本层节点数)行\(n^{[i-1]}\)(上层节点数)列的矩阵,也就是负责将上层节点的结果转成本层节点的结果。\(b^{[i]}\)自然是\(n^{[i]}\)行1列的向量了。最后再将结果各自丢进sigmod函数里面,不说了。
如果写出个通式的话也行:
\[\begin{align} z^{[i]} &= W^{[i]} a^{[i-1]} + b^{[i]} \\ a^{[i]} &= \sigma(z^{[i]}) \end{align}\]不过注意\(a^{[0]}\)就是输入值,没有放入sigmod函数里面。同时矩阵\(W^{[i]}\)是一个“行矩阵”,每一行是每一个节点的系数的转置\([\cdots w_i^{[1]T} \cdots]\)。
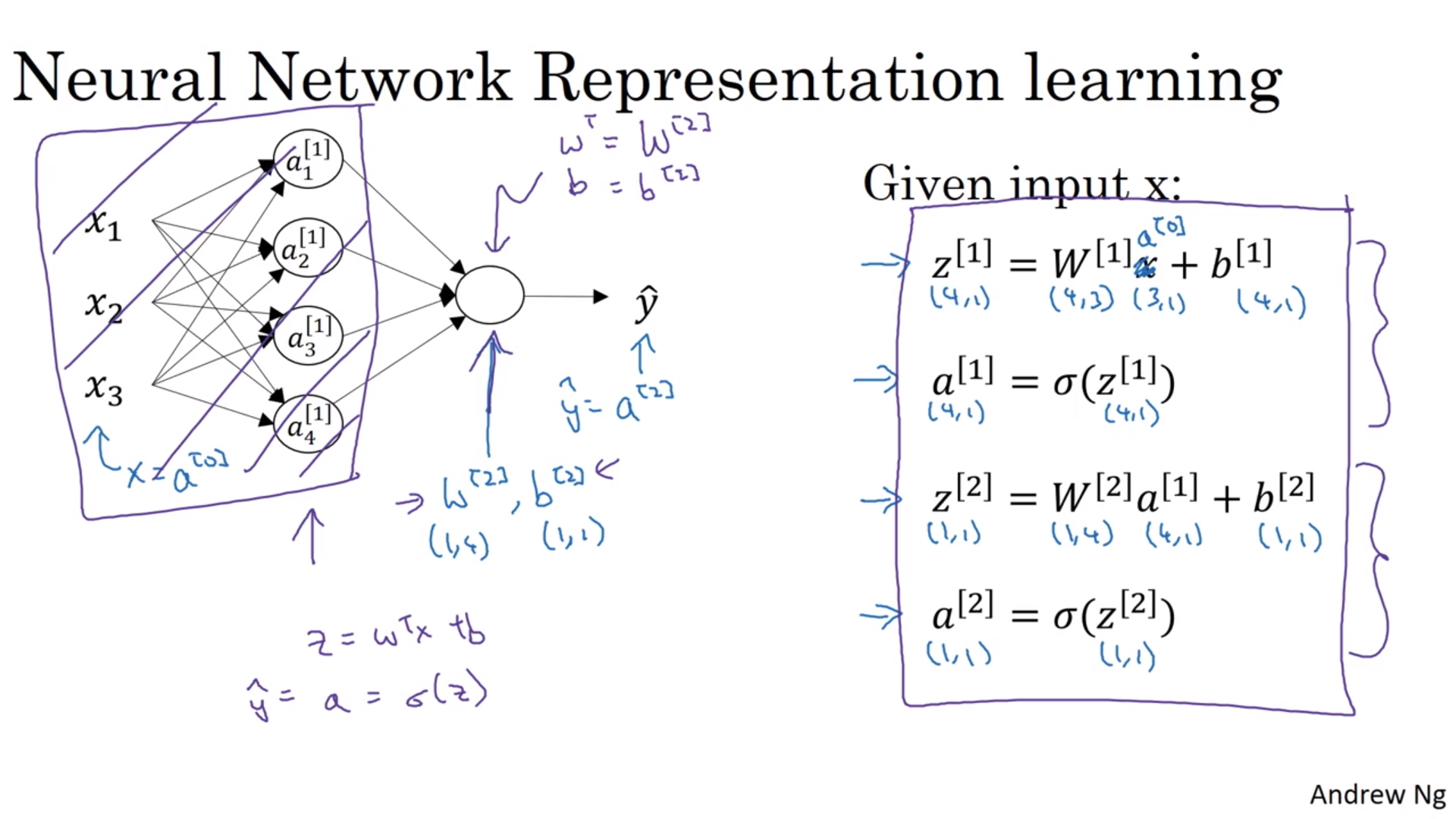
对于整个训练样本
当然可以继续矩阵化啦。把整个训练样本的列向量\(x,b\)排成一行(这也是惟一的排法了),结果\(z\)也这么做,然后大写,就变成了:
\[\begin{align} Z^{[1]} &= \begin{bmatrix} \vdots & \vdots & & \vdots \\ z^{[1](1)} & z^{[1](2)} & \cdots & z^{[1](m)} \\ \vdots & \vdots & & \vdots \\ \end{bmatrix} = \begin{bmatrix} \cdots w_1^{[1]T} \cdots \\ \cdots w_2^{[1]T} \cdots \\ \vdots \\ \cdots w_{[i]}^{[1]T} \cdots \end{bmatrix} \begin{bmatrix} \vdots & \vdots & & \vdots \\ x^{(1)} & x^{(2)} & \cdots & x^{(m)} \\ \vdots & \vdots & & \vdots \\ \end{bmatrix} + \begin{bmatrix} \vdots \\ b^{[1]} \\ \vdots \\ \end{bmatrix} \\ &= W^{[1]} X + b^{[1]} \end{align}\]或者对于某一层来说
\[\begin{align} Z^{[i]} &= \begin{bmatrix} \vdots & \vdots & & \vdots \\ z^{[i](1)} & z^{[i](2)} & \cdots & z^{[i](m)} \\ \vdots & \vdots & & \vdots \\ \end{bmatrix} = \begin{bmatrix} \cdots w_1^{[i]T} \cdots \\ \cdots w_2^{[i]T} \cdots \\ \vdots \\ \cdots w_{[i]}^{[i]T} \cdots \end{bmatrix} \begin{bmatrix} \vdots & \vdots & & \vdots \\ a^{[i](1)} & a^{[i](2)} & \cdots & a^{[i](m)} \\ \vdots & \vdots & & \vdots \\ \end{bmatrix} + \begin{bmatrix} \vdots \\ b^{[i]} \\ \vdots \\ \end{bmatrix} \\ &= W^{[i]} X + b^{[i]} \end{align}\]总结一下,\(Z^{[i]}\)是一个\(n^{[i]}\)行\(m\)列的矩阵,\(W^{[i]}\)是一个\(n^{[i]}\)行\(n^{[i-1]}\)列的矩阵,\(A^{[i]}\)是一个\(n^{[i]}\)行\(m\)列的矩阵,\(b^{[i]}\)本来应该也是一个\([i]\)行\(m\)列的矩阵(每列都是一样),但是在python里面,同行数的向量和矩阵相加时,向量会被自动展成相应的矩阵,所以也就不用写成大写的\(B^{[i]}\)了。可以留意的是向量/矩阵的偏导数和它自己有相同的形状。
通式:
\[\begin{align} Z^{[i]} &= W^{[i]} A^{[i-1]} + b^{[i]} \\ A^{[i]} &= \sigma(Z^{[i]}) \end{align}\]

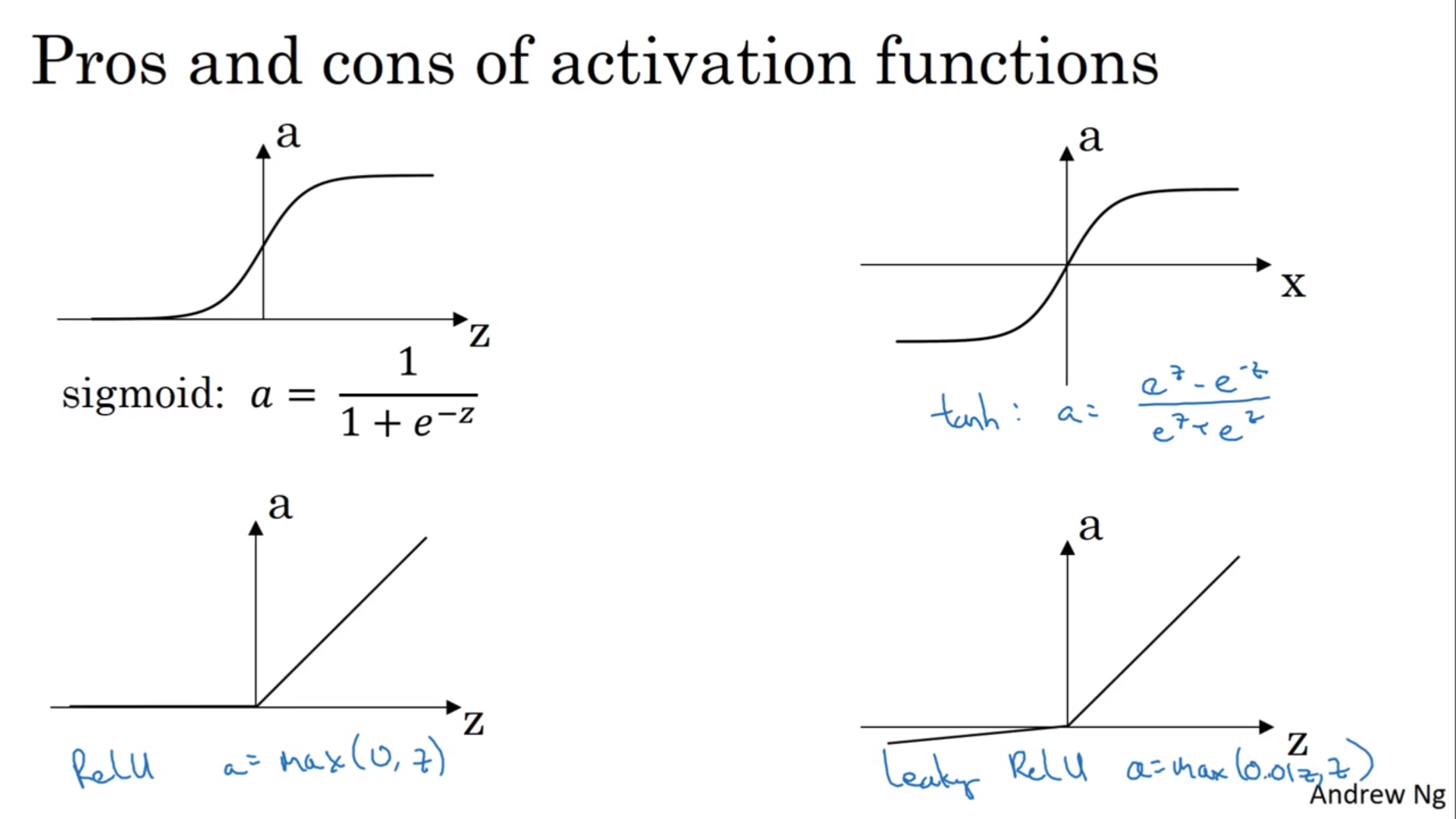
不同的activation function
sigmod函数的问题是它恒为正,所以算出来的结果不会关于0对称。所以隐藏层一般用\(\tanh(z)\)而不是sigmod,但是输出层还是用回sigmod。
但是\(\tanh(z)\)也还是有问题:当\(z\)很大的时候,斜率很小,所以会降低学习速率;所以也可以用RelU函数(折线),或者将RelU小于0的折线再改小一点。即使斜率为0实际上也还是可以的。
为什么activation function不是线性的?
也就是说为什么要给它套上一个奇怪的函数?
线性的AF意味着从头到脚都是线性的,也就没有意义(人又不是线性思考的233)。例外是在回归里面,当输出不在0到1之间的时候,最后一层可以用线性的。但是其他层还是要用非线性的。

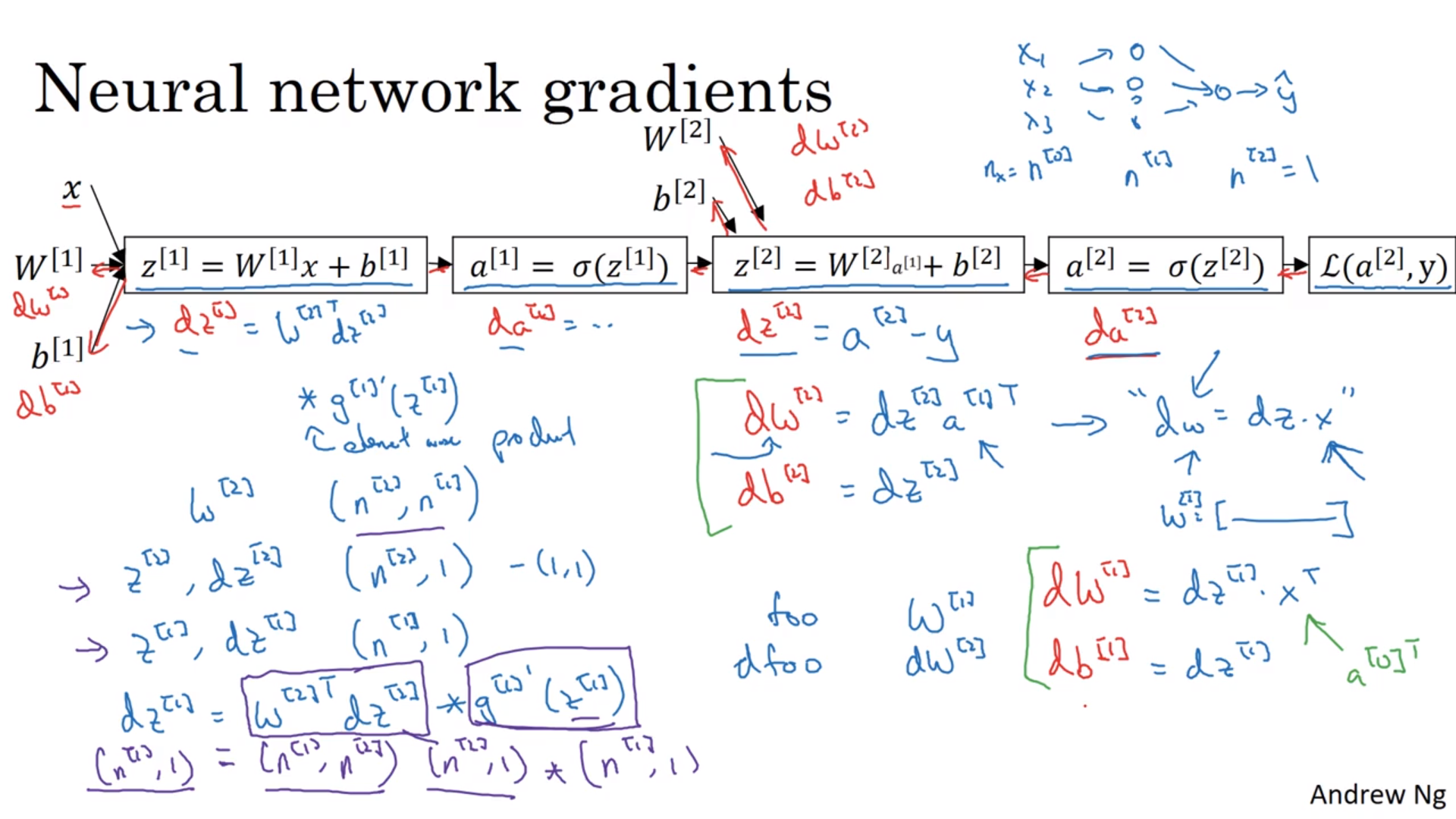
AF的导数
求就是了,又不是不会。按照链式反应(chain rule啦)来求就行了。按照之前的结论其实\(\frac{dL}{da^{[2]}}\)不用求,有\(\frac{dL}{dz^{[2]}} = a^{[2]} - y\)。
完全向量化之后出现的\(\frac{1}{m}\)以及求和是因为之前对某一个训练样本来说,只能计算损失函数;但是对于整个训练样本集来说,我们计算的是代价函数,而\(J = \frac{1}{m}\sum L\),所以多了点东西。

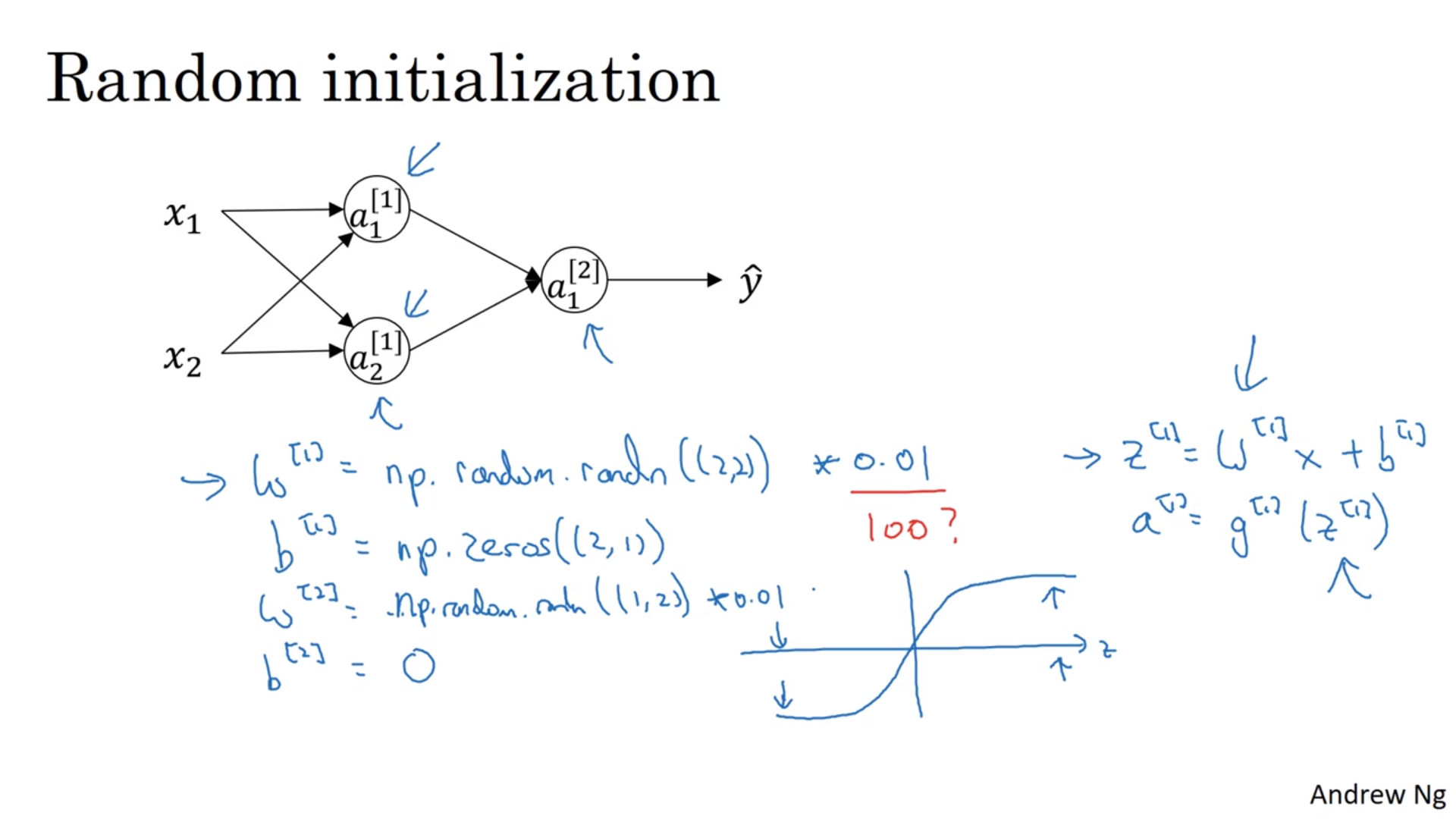
随机初值
参数全为0的话,所有的节点都是一样(对称)的,就没用了。所以要随机取值。一般会将\(w\)取为很小的高斯随机数,但是\(b\)没所谓。很小的高斯随机数是为了取到比较大的导数值,防止落到导数很靠近0的地方。
深神经网络
多层的神经网络和2层的其实是一样的,只不过多了一堆循环而已。
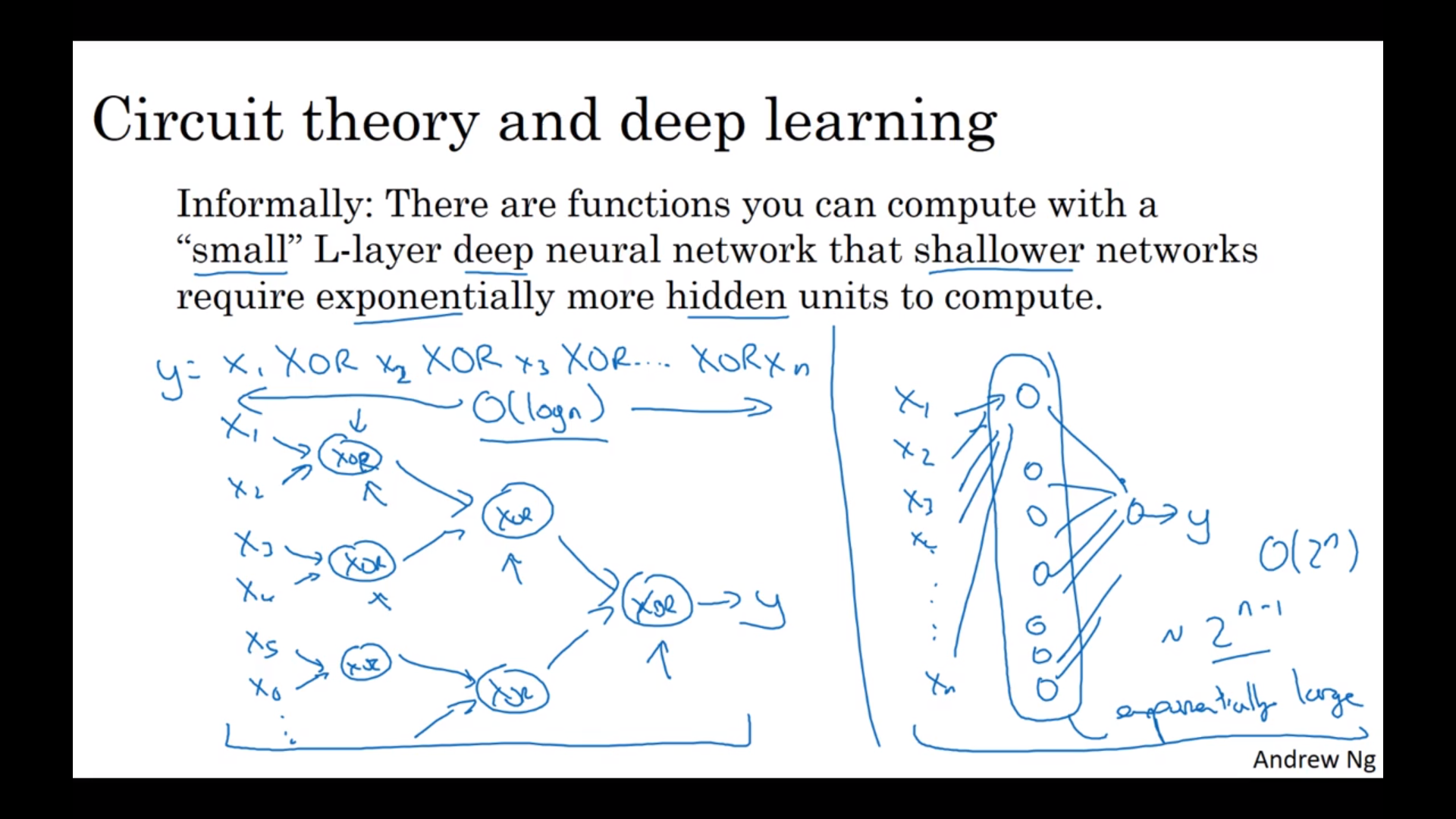
为什么要用深的神经网络?
层数从小到大:简单元素 -> 复杂元素。所以我们需要比较多层,但是每层里面的节点不一定多。
比单层的好用
正向传递
计算不同层数的时候可以用循环。
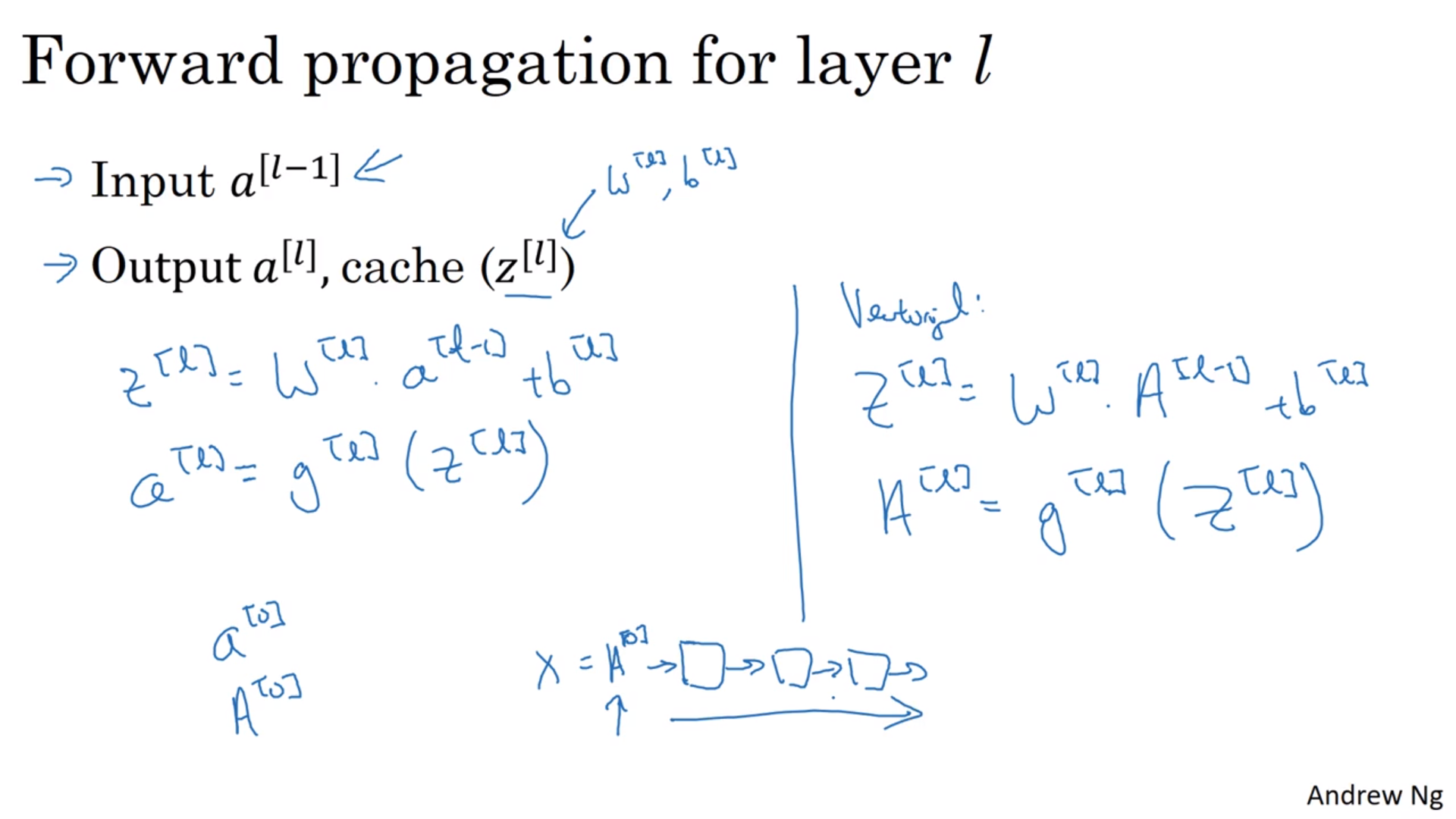
反向传递

具体做法
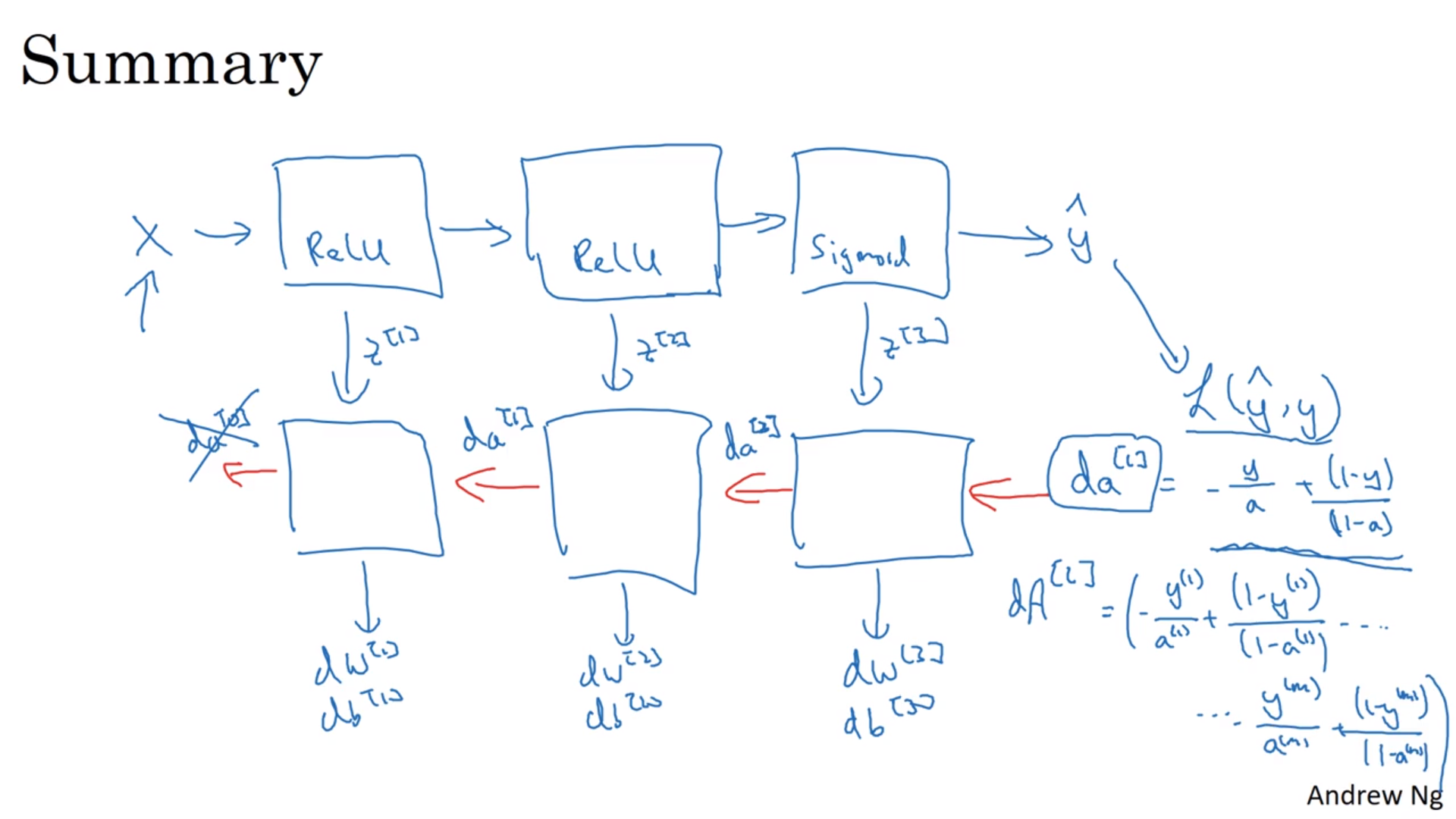
因为反向传递的时候有一个\(g'^{[l]}(z^{[l]})\),所以在正向传递的时候要将\(z^{[l]}\)记录下来。
参数和超参数
超参数:人为指定的参数
看超参数和\(J\)的关系(选多少的时候最小),是一个经验方法。最佳的超参数集可能会随着时间变化(电脑更新了)
这次的笔记本还演示了如何载入另外一个笔记本的函数。