问题
文中公式如果有编号则来自Radiative Transfer in Stellar and Planetary Atmospheres。
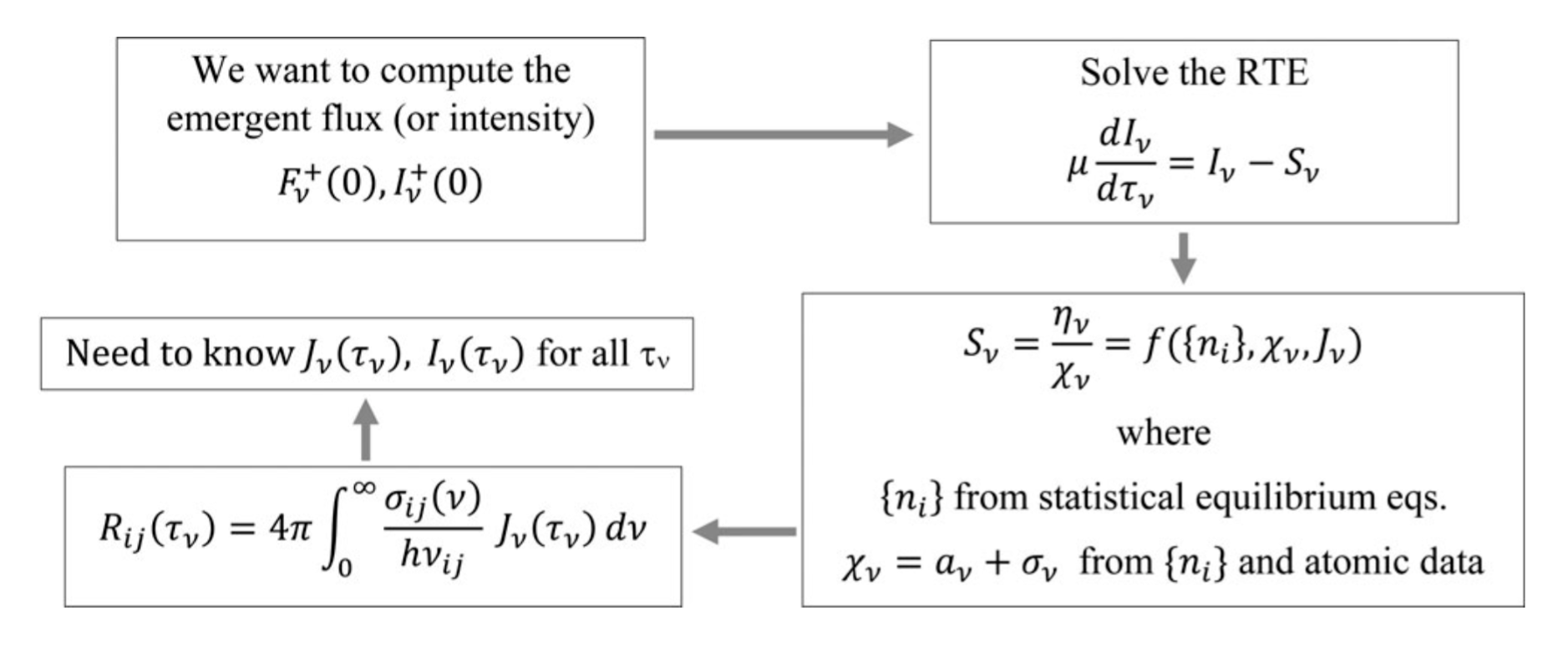
在算辐射转移方程的时候我们会遇到这样的一个循环:
 (Figure 2.10; Radiative Transfer in Stellar and Planetary Atmospheres)
(Figure 2.10; Radiative Transfer in Stellar and Planetary Atmospheres)
本质上就是源函数里面有辐射项(平均光强\(J_\nu\)),耦合在了一起所以不能独立解辐射转移方程。其中一个解决的办法就是利用平均光强的定义:
\[\begin{align} J_\nu(\tau_\nu) &= \frac{1}{2} \int_{-1}^1 I_\nu(\tau_\nu, \mu) d\mu \\ &= \frac{1}{2} \int_{0}^\infty S_\nu(t_\nu) E_1(|t_\nu - \tau_\nu|) dt_\nu \tag{2.49} \end{align}\]加上定义\(\Lambda\)算符:
\[\Lambda_{\tau_\nu} [f(t)] = \frac{1}{2} \int_0^\infty f(t) E_1(|t_\nu - \tau_\nu|) dt_\nu \tag{2.52}\]则有
\[J_\nu(\tau_\nu) = \Lambda_{\tau_\nu} [S_\nu(t_\nu)] \tag{2.53}\]在二能级原子下谱线的源函数可以写为:
\[S_\nu(\tau) = \epsilon B(T) + (1-\epsilon) J_\phi(\tau) = \epsilon B(T) + (1-\epsilon) \Lambda [S_\nu(t)] \tag{1.58, 3.65}\]谱线轮廓\(\phi\)被算进了\(\Lambda\)算符中。虽然可以求\(\Lambda\)算符的逆,但是这样计算量太大,所以就用\(\Lambda\)迭代来做。
对于这种形式的方程(源函数),它的解是一个叫做Neumann级数的东西。上网查了查中文的资料不多,基本上都是印度人讲的英文资料,就在这记录一下以便查阅。
Neumann级数
主要参考这里。
我们想解的是这样的一个方程:
\[y(x) = f(x) + \lambda \int_a^x K(x, t_1) y(t_1) dt_1\]其中\(f(x), K(x, t)\)已知,求\(y(x)\)。 这里简单假设各种函数的性质都良好,怎么积分都还有值而且不发散(其实就是懒)。
将上式中的\(y(t)\)不断展开,有:
\[\begin{align} y(x) &= f(x) + \lambda \int_a^x K(x, t_1) f(t_1) + \lambda \int_a^{t_1} K(t_1, t_2) y(t_2) dt_2 dt_1 \\ &= f(x) + \lambda \int_a^x K(x, t_1) f(t_1) dt_1 + \lambda^2 \int_a^x K(x, t_1) \int_a^{t_1} K(t_1, t_2) y(t_2) dt_2 dt_1\\ &= f(x) + \lambda \int_a^x K(x, t_1) f(t_1) dt_1 + \lambda^2 \int_a^x K(x, t_1) \int_a^{t_1} K(t_1, t_2) f(t_2) + \lambda \int_a^{t_2} K(t_2, t_3) y(t_3) dt_3 dt_2 dt_1 \\ &= f(x) + \lambda \int_a^x K(x, t_1) f(t_1) dt_1 + \lambda^2 \int_a^x K(x, t_1) \int_a^{t_1} K(t_1, t_2) f(t_2) dt_2 dt_1 + \lambda^2 \int_a^x K(x, t_1) \int_a^{t_1} K(t_1, t_2) f(t_2) \\ ~~~~+ \lambda \int_a^{t_2} K(t_2, t_3) y(t_3) dt_3 dt_2 dt_1 \end{align}\]我们来看上式最后一个等号的第二项(姑且叫做\(T_2\)):
\[\begin{align} T_2 &= \lambda^2 \int_a^x K(x, t_1) \int_a^{t_1} K(t_1, t_2) f(t_2) dt_2 dt_1 \\ &= \lambda^2 \int_a^x \int_{t_2}^x K(x, t_1)K(t_1, t_2) dt_1 f(t_2) dt_2 \\ &= \lambda^2 \int_a^x K_2(x, t_2) f(t_2) dt_2 \end{align}\]将\(K(t_1, t_2)\)叫做\(K_1(t_1, t_2)\),并将\(K_2(x, t_2)\)向更高次项推广,有
\[K_{n+1}(x, t) = \int_t^x K(x, z) K_n(z, t) dz\]并且
\[y(x) = f(x) + \int_a^x \left[ \sum_{n=1}^\infty \lambda^n K_n(x, t) \right] f(t) dt\]这个就是Neumann级数。
例子
解方程\(y(x) = e^{x^2} + \int_0^x e^{x^2-t^2} y(t) dt\)。
答案:\(y(x) = e^{x^2+x}\)。